题目内容
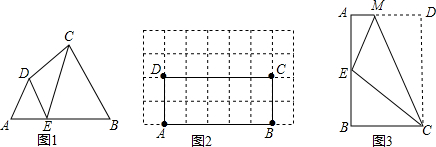
13.阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”:如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:(1)如图1,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
分析 (1)根据题意证明∠ADE=∠BEC和∠A=∠B,得到△ADE∽△BEC;
(2)根据题意画图即可;
(3)根据相似三角形的性质和折叠的性质解答即可.
解答 解:(1)∵∠A=∠DEC=45°
∴∠ADE+∠AED=135°,∠BEC+∠AED=135°,
∴∠ADE=∠BEC,
又∵∠A=∠B,
∴△ADE∽△BEC,
∴点E是四边形ABCD的边AB上的相似点;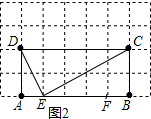
(2)如图中所示的点E和点F为AB上的强相似点;
(3)∵点E是四边形ABCM的边AB上的一个强相似点,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM,
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=$\frac{1}{3}$∠BCD=30°,CE=AB,
在Rt△BCE中,cos∠BCE=$\frac{BC}{EC}$,
∴$\frac{BC}{EC}$=$\frac{\sqrt{3}}{2}$,
∴$\frac{BC}{AB}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查的是相似三角形的综合应用,理解新定义、掌握相似三角形的性质定理是解题的关键.

练习册系列答案
相关题目
3.下列各数中:0、-$\sqrt{2}$、$\root{3}{8}$、$\frac{5}{13}$、π、0.3737737773…(它的位数无限且相邻两个“3”之间“7”的个数依次加1个),无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.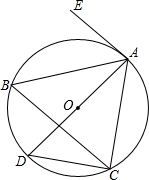 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
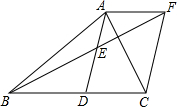 已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.
已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.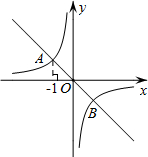 如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=$\frac{k}{x}$图象交于A,B两点,若点P在y轴上,且满足以点A,B,P为顶点的三角形是直角三角形,则点P的坐标是(0,$\sqrt{2}$)或(0,-$\sqrt{2}$)或(0,2)或(0,-2).
如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=$\frac{k}{x}$图象交于A,B两点,若点P在y轴上,且满足以点A,B,P为顶点的三角形是直角三角形,则点P的坐标是(0,$\sqrt{2}$)或(0,-$\sqrt{2}$)或(0,2)或(0,-2).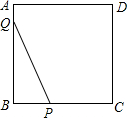 如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为3π.
如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为3π.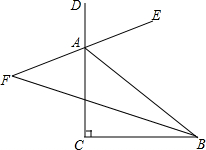 如图,在△ABC中,∠C=90°,∠ABC的平分线与外角∠BAD的平分线的反向延长线交于点F,则∠F=45°.
如图,在△ABC中,∠C=90°,∠ABC的平分线与外角∠BAD的平分线的反向延长线交于点F,则∠F=45°.