题目内容
15.已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示:| X | -2 | -1 | 0 |
| y | 3 | 2 | 1 |
| A. | x>-1 | B. | x<1 | C. | x>-3 | D. | x>1 |
分析 首先求出一次函数的解析式,由k、b的值确定图象经过的象限,根据与图象交点的坐标即可求出答案.
解答 解:把(-1,2),(0,1)代入y=kx+b得:$\left\{\begin{array}{l}{2=-k+b}\\{1=b}\end{array}\right.$,
解得:k=-1,b=1,
∴y1=-x+1,y2=x-1,
∵y1=-x+1,y2=x-1都交于(1,0)点,y1=-x+1图象经过一二四象限,y2=x-1图象经过一三四象限,
∴不等式kx+b<bx+k的解集为是x>1.
故选D.
点评 本题主要考查了一次函数与一元一次不等式,待定系数法求一次函数的解析式等知识点,解此题的关键是能根据图象确定一元一次不等式的解集.用的数学思想是数形结合的思想.

练习册系列答案
相关题目
20.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{{m}^{2}+{n}^{2}}$ | B. | $\sqrt{9a}$ | C. | $\sqrt{\frac{a}{3}}$ | D. | $\sqrt{0.2}$ |
5.下列运算正确的是( )
| A. | x3+x2=x5 | B. | 2x3-x3=1 | C. | x2•x3=x6 | D. | x6÷x3=x3 |
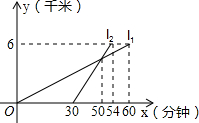 某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,他们都沿相同路线前往.如图,已知a、b分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,请你根据图中提供的信息,写出三个正确结论.
某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,他们都沿相同路线前往.如图,已知a、b分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,请你根据图中提供的信息,写出三个正确结论.