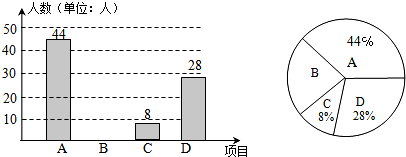
如果$\frac{a}{b}$=$\frac{c}{d}$.那么$\frac{a+2b}{2a-b}$=$\frac{c+2d}{2c-d}$．题目和参考答案——青夏教育精英家教网—

题目内容

14．如果$\frac{a}{b}$=$\frac{c}{d}$，那么$\frac{a+2b}{2a-b}$=$\frac{c+2d}{2c-d}$．

分析根据比例的性质，可用b表示a，根据分式的性质，可得答案．

解答解：由$\frac{a}{b}$=$\frac{c}{d}$，得
a=$\frac{c}{d}$b．
$\frac{a+2b}{2a-b}$=$\frac{\frac{c}{d}b+2b}{2\frac{c}{d}b-b}$=$\frac{c+2d}{2c-d}$，
故答案为：$\frac{c+2d}{2c-d}$．

点评本题考查了比例的性质，利用比例的性质得出b表示a是解题关键，又利用了分式的性质．

练习册系列答案

小学升学多轮夯基总复习系列答案

金钥匙期末冲刺100分系列答案

名师指导期末冲刺卷系列答案

初中英语听力训练苏州大学出版社系列答案

相关题目

4．

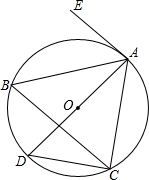如图，⊙O是△ABC的外接圆，AD是⊙O的直径，EA是⊙O的切线．若∠EAC=120°，则∠ABC的度数是（　　）

5．我们已经知道函数y=$\frac{1}{x}$与y=-$\frac{1}{x}$的两个图象之间的联系与区别，那你知道函数y=$\frac{1}{|x|}$的图象与上述两个函数图象之间又有怎样的关系吗？
（1）试用描点法画出图象加以探究；
（2）如果利用y=$\frac{1}{|x|}$与y=$\frac{1}{x}$或y=-$\frac{1}{x}$的图象之间的关系，可怎样画y=-$\frac{2}{|x|}$的图象？

2．

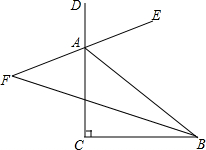如图，在△ABC中，∠C=90°，∠ABC的平分线与外角∠BAD的平分线的反向延长线交于点F，则∠F=45°．

9．

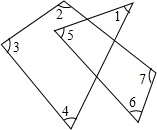如图，求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数．

19．计算：（式子中的字母均为正数）
（1）（2a${\;}^{\frac{2}{3}}$b${\;}^{\frac{1}{2}}$）（-6a${\;}^{\frac{1}{2}}$b${\;}^{\frac{1}{3}}$）÷（-3a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$）（a${\;}^{-\frac{3}{8}}$b${\;}^{\frac{1}{4}}$）⁸．
（2）a${\;}^{\frac{1}{3}}$a${\;}^{\frac{3}{4}}$a${\;}^{\frac{7}{12}}$；
（3）a${\;}^{\frac{2}{3}}$a${\;}^{\frac{3}{4}}$÷a${\;}^{\frac{5}{6}}$；
（4）（x${\;}^{\frac{1}{3}}$y${\;}^{-\frac{3}{4}}$）¹²．

6．已知（x+1）⁴=a₄x⁴+a₃x³+a₂x²+a₁x+a₀，那么你能否求出a₀+a₁+a₂+a₃+a₄+a₅+a₆和a₀+a₂+a₄的值？若能，求出其值；若不能，说明理由．

3．当x=$\frac{1}{3}$时，代数式3x²-2x+1有最小值，这个值是$\frac{2}{3}$．

4．在某市开展的“体育、艺术2+1”活动中，某校根据实际情况，决定主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳这四种运动项目．为了解学生喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图．请你结合图中的信息解答下列问题．
（1）样本中喜欢B项目的人数百分比是20%，其所在扇形统计图中的圆心角的度数是72°；
（2）求出所抽取的学生人数，并把条形统计图补充完整；
（3）已知该校有1000人，根据样本估计全校喜欢跳绳的人数是多少？

试题分类