题目内容
20.如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+$\frac{3}{2}$与y=x相交于点A,与x轴交于点B.(1)求点A,B的坐标;
(2)在平面直角坐标系xOy中,是否存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形?如果存在,试求出所有符合条件的点C的坐标;如果不存在,请说明理由;
(3)在直线OA上,是否存在一点D,使得△DOB是等腰三角形?如果存在,试求出所有符合条件的点D的坐标,如果不存在,请说明理由.
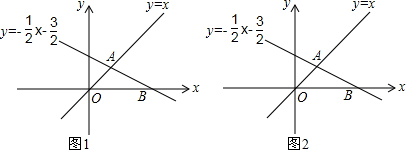
分析 (1)把直线y=-$\frac{1}{2}$x+$\frac{3}{2}$与y=x联立得出方程组求解即可得出点A的坐标,由直线y=-$\frac{1}{2}$x+$\frac{3}{2}$与x轴交于点B,令y=0,求出x的值,即可得出B的坐标,
(2)存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形.分三种情况①过点A作平行于x轴的直线,过点O作平行于AB的直线,两直线交于点C,②过点A作平行于x轴的直线,过点B作平行于AO的直线,两直线交于点C,③过点O作平行于AB轴的直线,过点B作平行于AO的直线,两直线交于点C分别求解即可,
(3)在直线OA上,存在一点D,使得△DOB是等腰三角形,分四种情况①当OB=OD时,②当OD=OB时,③当OB=DB时,④如图7,当DO=DB时分别求解即可.
解答 解:(1)∵直线y=-$\frac{1}{2}$x+$\frac{3}{2}$与y=x相交于点A,
∴联立得$\left\{\begin{array}{l}{y=-\frac{1}{2}x+\frac{3}{2}}\\{y=x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
∴点A(1,1),
∵直线y=-$\frac{1}{2}$x+$\frac{3}{2}$与x轴交于点B,
∴令y=0,得-$\frac{1}{2}$x+$\frac{3}{2}$=0,解得x=3,
∴B(3,0),
(2)存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形.
①如图1,过点A作平行于x轴的直线,过点O作平行于AB的直线,两直线交于点C,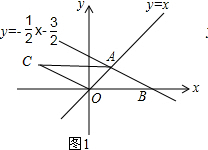
∵AC∥x轴,OC∥AB,
∴四边形CABO是平行四边形,
∵A(1,1),B(3,0),
∴AC=OB=3,
∴C(-2,1),
②如图2,过点A作平行于x轴的直线,过点B作平行于AO的直线,两直线交于点C,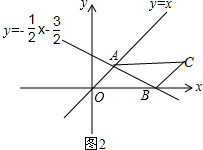
∵AC∥x轴,BC∥AO,
∴四边形CAOB是平行四边形,
∵A(1,1),B(3,0),
∴AC=OB=3,
∴C(4,1),
③如图3,过点O作平行于AB轴的直线,过点B作平行于AO的直线,两直线交于点C,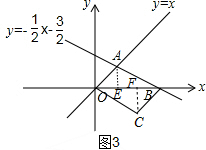
∵OC∥AB,BC∥AO,
∴四边形CBAO是平行四边形,
∵A(1,1),B(3,0),
∴AO=BC,OC=AB,
作AE⊥OB,CF⊥OB,易得OE=EF=FB=1,
∴C(2,-1),
(3)在直线OA上,存在一点D,使得△DOB是等腰三角形,
①如图4,当OB=OD时,作DE⊥x轴,交x轴于点E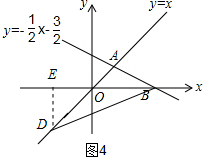
∵OB=3,点D在OA上,∠DOE=45°
∴DE=OE=$\frac{3\sqrt{2}}{2}$,
∴D(-$\frac{3\sqrt{2}}{2}$,-$\frac{3\sqrt{2}}{2}$),
②如图5,当OD=OB时,作DE⊥x轴,交x轴于点E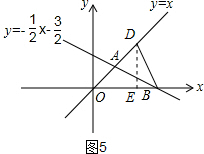
∵OB=3,点D在OA上,∠DOE=45°
∴DE=OE=$\frac{3\sqrt{2}}{2}$,
∴D($\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$),
③如图6,当OB=DB时,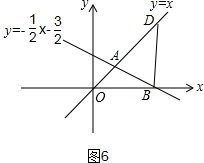
∵∠AOB=∠ODB=45°,
∴DB⊥OB,
∵OB=3,
∴D(3,3),
④如图7,当DO=DB时,作DE⊥x轴,交x轴于点E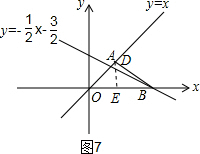
∵∠AOB=∠OBD=45°,
∴OD⊥DB,
∵OB=3,
∴OE=$\frac{3}{2}$,AE=$\frac{3}{2}$,
∴D($\frac{3}{2}$,$\frac{3}{2}$).
综上所述,在直线OA上,存在点D(-$\frac{3\sqrt{2}}{2}$,-$\frac{3\sqrt{2}}{2}$),D($\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$),D(3,3)或D($\frac{3}{2}$,$\frac{3}{2}$),使得△DOB是等腰三角形,
点评 本题主要考查了一次函数的综合题,涉及一次函数的性质,等腰三角形的性质及平行四边形的判定,性质,解题的关键是能正确分不同种情况作图,解析,一定不要漏解.

 名校课堂系列答案
名校课堂系列答案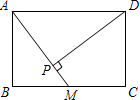 如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,则点D到AM的距离DP的长为$\frac{24}{5}$.
如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,则点D到AM的距离DP的长为$\frac{24}{5}$.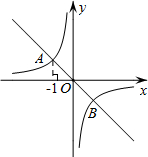 如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=$\frac{k}{x}$图象交于A,B两点,若点P在y轴上,且满足以点A,B,P为顶点的三角形是直角三角形,则点P的坐标是(0,$\sqrt{2}$)或(0,-$\sqrt{2}$)或(0,2)或(0,-2).
如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=$\frac{k}{x}$图象交于A,B两点,若点P在y轴上,且满足以点A,B,P为顶点的三角形是直角三角形,则点P的坐标是(0,$\sqrt{2}$)或(0,-$\sqrt{2}$)或(0,2)或(0,-2). 平行四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,则图中共有平行四边形的个数是( )
平行四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,则图中共有平行四边形的个数是( )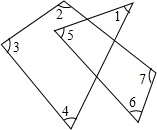 如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.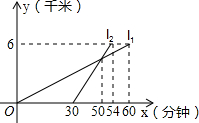 某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,他们都沿相同路线前往.如图,已知a、b分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,请你根据图中提供的信息,写出三个正确结论.
某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,他们都沿相同路线前往.如图,已知a、b分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,请你根据图中提供的信息,写出三个正确结论.