题目内容
18.(1)计算:${(-1)^2}+{sin^2}30°+(\sqrt{2})^0-{(\frac{1}{2})^{-1}}$(2)解不等式组$\left\{\begin{array}{l}{3x+1<x-3①}\\{\frac{1+x}{2}≤\frac{1+2x}{3}+1②}\end{array}$并写出它的所有整数解.
分析 (1)原式利用乘方的意义,特殊角的三角函数值,以及零指数幂、负整数指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,即可求出所有整数解.
解答 解:(1)原式=1+$\frac{1}{4}$+1-2=$\frac{1}{4}$;
(2)由①得:2x<-4,
解得:x<-2,
由②得:3(1+x)≤2(1+2x)+6,
去括号得:3+3x≤2+4x+6,
移项合并得:-x≤5,
解得:x≥-5,
∴不等式组的解集为-5≤x<-2,
则不等式组的整数解为-5,-4,-3.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
10.已知a,b,c为△ABC的三条边,化简 $\sqrt{(a+b-c)^{2}}$-|b-a-c|=( )
| A. | b+c | B. | 0 | C. | b-c | D. | 2b-2c |
7.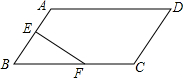 如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为( )
如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为( )
 如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为( )
如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为( )| A. | 1:4 | B. | 1:8 | C. | 1:5 | D. | 1:7 |