题目内容
18.求下列函数中自变量x的取值范围(1)y=$\sqrt{\frac{1}{x+2}}$
(2)y=$\sqrt{x-2}$+$\sqrt{2-x}$
(3)y=$\sqrt{(x+2)^{2}}$
(4)y=$\sqrt{-(x-2)^{2}}$
(5)y=$\frac{-\sqrt{x+1}}{x-2}$.
分析 (1)根据二次根式的被开方数不小于零,分母不为零即可求解;
(2)根据二次根式的被开方数不小于零即可求解;
(3)根据二次根式的被开方数不小于零即可求解;
(4)根据二次根式的被开方数不小于零即可求解;
(5)根据二次根式的被开方数不小于零,分母不为零即可求解.
解答 解:(1)依题意有x+2>0,
解得x>-2;
(2)依题意有x-2≥0且2-x≥0,
解得x=2;
(3)依题意有(x-2)2≥0,
解得x为任意实数;
(4)依题意有-(x-2)2≥0,
解得x=2;
(5)依题意有x+1≥0且x-2≠0,
解得x≥-1且x≠2.
点评 考查了函数自变量的取值范围,自变量的取值范围必须使含有自变量的表达式都有意义.
①当表达式的分母不含有自变量时,自变量取全体实数.
②当表达式的分母中含有自变量时,自变量取值要使分母不为零.
③当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.
④对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.

练习册系列答案
相关题目
8.函数$y=\frac{x}{x+3}$中,自变量x的取值范围是( )
| A. | x>-3 | B. | x<-3 | C. | x≠-3 | D. | x≠3 |
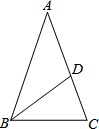 如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一).
如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一).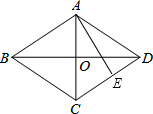 如图,菱形花坛ABCD的边长为20m,DE=CE,AE⊥CD,沿对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
如图,菱形花坛ABCD的边长为20m,DE=CE,AE⊥CD,沿对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积. 如图,把矩形ABCD沿对角线CD折叠,使点C落在C′处,BC′交AD于E.
如图,把矩形ABCD沿对角线CD折叠,使点C落在C′处,BC′交AD于E.