题目内容
 如图,已知⊙O的半径为
如图,已知⊙O的半径为| 10 |
考点:垂径定理,圆周角定理,解直角三角形
专题:
分析:连接OA、OB,由于OM⊥AB,根据垂径定理易证得∠BOM=
∠AOB,而由圆周角定理可得∠C=
∠AOB=∠BOM,因此∠CBD=∠OBM,只需求得∠OBM的正弦值即可;在Rt△OBM中,由垂径定理可得BM=4,已知⊙O的半径OB=5,由勾股定理可求得OM=3,即可求出∠OBM即∠CBD得正弦值,由此得解.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: 连接OA、OB;
连接OA、OB;
∵OM⊥AB,
∴AM=BM=3,∠AOM=∠BOM=
∠AOB;
又∵∠C=
∠AOB,
∴∠BOM=∠BCD,∠OBM=∠CBD;
在Rt△OBM中,
∵OB=
,BM=3,
∴OM=
=
=1,
∴sin∠OBM=sin∠CBD=
=
=
.
 连接OA、OB;
连接OA、OB;∵OM⊥AB,
∴AM=BM=3,∠AOM=∠BOM=
| 1 |
| 2 |
又∵∠C=
| 1 |
| 2 |
∴∠BOM=∠BCD,∠OBM=∠CBD;
在Rt△OBM中,
∵OB=
| 10 |
∴OM=
| OB2-BM2 |
| 10-9 |
∴sin∠OBM=sin∠CBD=
| OM |
| OB |
| 1 | ||
|
| ||
| 10 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 下列四个图案中,可以通过如图平移得到的是( )
下列四个图案中,可以通过如图平移得到的是( )A、 |
B、 |
C、 |
D、 |
在锐角三角形ABC中,BC>AB>AC,小靖依下列方法作图:
(1)作∠A的平分线交BC于D点.
(2)作AD的中垂线交AC于E点.
(3)连接DE.
根据他画的图形,下列关系正确的是( )
(1)作∠A的平分线交BC于D点.
(2)作AD的中垂线交AC于E点.
(3)连接DE.
根据他画的图形,下列关系正确的是( )
| A、DE∥AB |
| B、DE⊥AC |
| C、CD=DE |
| D、CD=BD |
点A(-2,m)与点B(n,4)关于原点对称,则m+n的值是( )
| A、2 | B、6 | C、-2 | D、-6 |
 如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6.求证:BA⊥AD.
如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6.求证:BA⊥AD. 如图,在方格纸中,cos(α+β)=
如图,在方格纸中,cos(α+β)=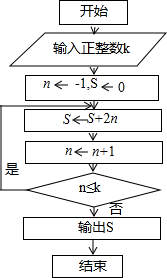 在计算机科学中常用框图表示程序运行的顺序,称程序流程图.(如图所示,箭头表示执行的顺序或数据的流向,如n←n+1表示将n的值增加1后仍赋给n)执行如图的流程图,如果输入的K=10,那么输出的S=
在计算机科学中常用框图表示程序运行的顺序,称程序流程图.(如图所示,箭头表示执行的顺序或数据的流向,如n←n+1表示将n的值增加1后仍赋给n)执行如图的流程图,如果输入的K=10,那么输出的S= 已知,如图,在?ABCD中,AD⊥BD,点E,F分别在AB,BD上,且满足AD=AE=DF,连接DE,AF,EF.
已知,如图,在?ABCD中,AD⊥BD,点E,F分别在AB,BD上,且满足AD=AE=DF,连接DE,AF,EF.