��Ŀ����
15�� ��ͼ��ֱ��AB��x�ᡢy��ֱ���B��A���㣬�߶�OA��OB�ij��ǹ���x��һԪ���η���x2-14x+48=0����������OA��OB��
��ͼ��ֱ��AB��x�ᡢy��ֱ���B��A���㣬�߶�OA��OB�ij��ǹ���x��һԪ���η���x2-14x+48=0����������OA��OB�������������⣺
��1�����߶�AB�ij���
��2����C��ֱ��AB��һ�㣬��3S��OBC=2S��OAC����ֱ��OC�ĺ�������ʽ��
��3���ڣ�2�������£���C���߶�AB�ϵĵ㣬��ֱ��AB���Ƿ���ڵ�P��ʹ�Ե�O��C��PΪ�������������ֱ�������Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1�����Ƚⷽ�����OA��OB�ij���Ȼ�����ù��ɶ������AB�ij����ɣ�
��2�����ݵ�A�͵�B������ó�ֱ��AB�Ľ���ʽ���������C�����꣬���������ʽ��ɣ�
��3������ֱ�������εó���P�����꼴�ɣ�
��� ��1���⣺����x2-14x+48=0����Ϊ��
��x-6����x-8��=0��
��ã�x1=6��x2=8��
��OA��OB��
��OA=6��OB=8��
��AB=$\sqrt{O{A}^{2}+O{B}^{2}}=10$��
��2����ֱ��AB�Ľ���ʽΪ��y=kx+b��
��B��-8��0����A��0��6���������ʽ�У��ã�$\left\{\begin{array}{l}{-8k+b=0}\\{b=6}\end{array}\right.$��
��ã�k=$\frac{3}{4}$��b=6��
����ֱ�ߵĽ���ʽ��y=$\frac{3}{4}$x+6��
���Ե�C������Ϊ��x��$\frac{3}{4}x+6$����
��Ϊ3S��OBC=2S��OAC��
���Կɵ�S��OAC=6����x����$\frac{1}{2}$=��3x
S��OBC=8��$\frac{3}{4}x+6$��•$\frac{1}{2}$=����3x+24��
��S��OBC=2S��OACʱ��x=$\frac{24}{5}$��x=-24
��LOC��y1=-$\frac{1}{2}$x��
�ɵý���ʽΪ��y2=$\frac{1}{2}$x��
��3������C������Ϊ��-24��-12��ʱ��ʹ��O��C��PΪ�������������ֱ�������Σ�
��ɵõ�P������Ϊ��$\frac{24}{5}��\frac{48}{5}$����
����C������Ϊ��$\frac{24}{5}��\frac{48}{5}$��ʱ��ʹ��O��C��PΪ�������������ֱ�������Σ�
��ɵõ�P������Ϊ��$-\frac{72}{15}��\frac{32}{5}$����
������������P��������$\frac{24}{5}��\frac{48}{5}$����$-\frac{72}{15}��\frac{32}{5}$����
���� ���⿼����һ�κ������ۺ�֪ʶ����Ŀ�н����˵������������ε������ת�������ǽ������Ĺؼ����Ѷ��е�ƫ�ϣ�

 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�| A�� | a��5��a��-2 | B�� | -2��a��5 | C�� | -2��a��5 | D�� | a��5��a��-2 |
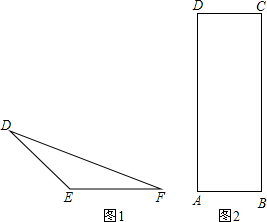 ��ͼ���ڵ���������DEF�У�DE=FE=1����DEF=135�㣮
��ͼ���ڵ���������DEF�У�DE=FE=1����DEF=135�㣮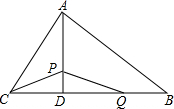 ��ͼ���ڡ�ABC�У���AD����BC�ڵ�D��AD=12cm��BD=16cm��CD=8cm������P�ӵ�D������������D-A-B���յ�B�˶�����P��AD�ϵ��ٶ�4cm/s����AB�ϵ��ٶ�5cm/s��ͬʱ��Q�ӵ�B��������6cm/s���ٶȣ���BC���յ�C�˶�������Qֹͣ�˶�ʱ����PҲ��ֹ֮ͣ�����P���˶�ʱ��Ϊt��s����
��ͼ���ڡ�ABC�У���AD����BC�ڵ�D��AD=12cm��BD=16cm��CD=8cm������P�ӵ�D������������D-A-B���յ�B�˶�����P��AD�ϵ��ٶ�4cm/s����AB�ϵ��ٶ�5cm/s��ͬʱ��Q�ӵ�B��������6cm/s���ٶȣ���BC���յ�C�˶�������Qֹͣ�˶�ʱ����PҲ��ֹ֮ͣ�����P���˶�ʱ��Ϊt��s����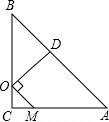 ��ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=7����O��BC�ϣ���CO=1����M��AC��һ���㣬����OM�����߶�OM�Ƶ�O��ʱ����ת90�㣬�õ��߶�OD��Ҫʹ��Dǡ������AB�ϣ�CM�ij���Ϊ5��
��ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=7����O��BC�ϣ���CO=1����M��AC��һ���㣬����OM�����߶�OM�Ƶ�O��ʱ����ת90�㣬�õ��߶�OD��Ҫʹ��Dǡ������AB�ϣ�CM�ij���Ϊ5��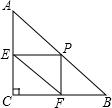 ��ͼ���ڡ�ABC�У���C=90�㣬AB=10��$\frac{BC}{AC}$=$\frac{3}{4}$����AB����һ��P��PE��AC�ڵ�E��PF��BC�ڵ�F����EF����Сֵ��$\frac{24}{5}$��
��ͼ���ڡ�ABC�У���C=90�㣬AB=10��$\frac{BC}{AC}$=$\frac{3}{4}$����AB����һ��P��PE��AC�ڵ�E��PF��BC�ڵ�F����EF����Сֵ��$\frac{24}{5}$��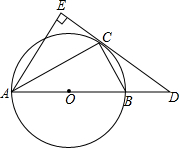 ��ͼ����֪��O�ǡ�ABC�����Բ��AB�ǡ�O��ֱ����D��AB�ӳ����ϵ�һ�㣬AE��DC��DC���ӳ�����E��ACƽ�֡�DAE��
��ͼ����֪��O�ǡ�ABC�����Բ��AB�ǡ�O��ֱ����D��AB�ӳ����ϵ�һ�㣬AE��DC��DC���ӳ�����E��ACƽ�֡�DAE��