题目内容
15. 如图,每个小正方形的边长为1,A、B、C为小正方形的顶点,求证:∠ABC=45°.
如图,每个小正方形的边长为1,A、B、C为小正方形的顶点,求证:∠ABC=45°.
分析 连结AC,先依据勾股定理求得AB、AC、BC的长,然后依据勾股定理的逆定理可求得△ABC为直角三角形,然后依据AC=BC可得到三角形ABC为等腰直角三角形,故此可得到∠ABC=45°.
解答 证明:连接AC,则由勾股定理可以得到:AC=$\sqrt{5}$,BC=$\sqrt{5}$,AB=$\sqrt{10}$.
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
又∵AC=BC,
∴∠CAB=∠ABC.
∴∠ABC=45°.
点评 本题主要考查的是勾股定理和勾股定理的逆定理的应用,等腰直角三角形的判定,证得△ABC为直角三角形是解题的关键.

练习册系列答案
相关题目
18.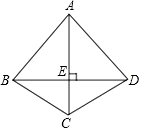 如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
 如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )| A. | AC平分∠BCD | B. | AB=BD | C. | △BEC≌△DEC | D. | BC=DC |
5.相似三角形的概念是( )
| A. | 对应角相等、对应边成比例的两个三角形 | |
| B. | 两角分别相等的两个三角形 | |
| C. | 三边对应成比例的两个三角形 | |
| D. | 两边对应成比例且夹角相等的两个三角形 |
 如图所示,⊙O的直径AB和弦CD交于E,已知AE=8,EB=2,∠CEA=30°,求CD的长.
如图所示,⊙O的直径AB和弦CD交于E,已知AE=8,EB=2,∠CEA=30°,求CD的长. 如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半径是2,则OD的长为2$\sqrt{3}$.
如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半径是2,则OD的长为2$\sqrt{3}$.