题目内容
2. 如图,在Rt△ABC中,斜边上的高AD=3,cosB=$\frac{4}{5}$,则AC=$\frac{15}{4}$.
如图,在Rt△ABC中,斜边上的高AD=3,cosB=$\frac{4}{5}$,则AC=$\frac{15}{4}$.
分析 先根据等角的余角相等得到∠DAC=∠B,则cos∠DAC=cosB,在Rt△ADC中,根据余弦的定义得cos∠DAC=$\frac{AD}{AC}$=$\frac{4}{5}$,然后把AD=3代入计算即可.
解答 解:∵AD⊥BC,
∴∠B+∠BAD=90°,
∵∠BAD+∠DAC=90°,
∴∠DAC=∠B,
∴cos∠DAC=cosB,
在Rt△ADC中,cos∠DAC=$\frac{AD}{AC}$=$\frac{4}{5}$,
而AD=3,
∴AC=$\frac{15}{4}$.
故答案为$\frac{15}{4}$.
点评 本题考查了解直角三角形,解题的关键是将∠B的余弦值转化为∠DAC余弦值,从而将已知条件融合到一个直角三角形中求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知关于x,y的方程组$\left\{\begin{array}{l}{{x}^{2}+y=25}\\{6x-y=k}\end{array}\right.$ 无实数解,则k的取值范围为k>34.
12. 有理数a、b在数轴上的对应的位置如图所示,则下列各式中正确的是( )
有理数a、b在数轴上的对应的位置如图所示,则下列各式中正确的是( )
 有理数a、b在数轴上的对应的位置如图所示,则下列各式中正确的是( )
有理数a、b在数轴上的对应的位置如图所示,则下列各式中正确的是( )| A. | a+b<0 | B. | a+b>0 | C. | a-b=0 | D. | a-b>0 |
9.下列各组数中,以它们为边长的线段能构成直角三角形的是( )
| A. | 5,12,13 | B. | 5,6,7 | C. | 1,4,9 | D. | 5,11,12 |
12. 如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
 如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )| A. | 105° | B. | 100° | C. | 95° | D. | 90° |
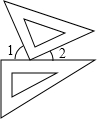 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,设∠1=x°,∠2=y°,先根据题意列出二元一次方程组,再求解.
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,设∠1=x°,∠2=y°,先根据题意列出二元一次方程组,再求解. 在△ABC中,AD⊥BC于点D,BD=8,AD=6,S△ABC=42,那么AC的长为6$\sqrt{2}$.
在△ABC中,AD⊥BC于点D,BD=8,AD=6,S△ABC=42,那么AC的长为6$\sqrt{2}$.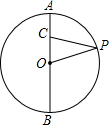 如图,点C在⊙O的直径AB上,AB=6,AC=1.点P为⊙O上的任意一点,当∠OPC取最大值时,则△OCP的面积为$\sqrt{5}$.
如图,点C在⊙O的直径AB上,AB=6,AC=1.点P为⊙O上的任意一点,当∠OPC取最大值时,则△OCP的面积为$\sqrt{5}$. 在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,直线CD过点O.
在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,直线CD过点O.