题目内容
14.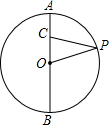 如图,点C在⊙O的直径AB上,AB=6,AC=1.点P为⊙O上的任意一点,当∠OPC取最大值时,则△OCP的面积为$\sqrt{5}$.
如图,点C在⊙O的直径AB上,AB=6,AC=1.点P为⊙O上的任意一点,当∠OPC取最大值时,则△OCP的面积为$\sqrt{5}$.
分析 先确定其∠OPC取最大值时点P的位置:PC⊥AB时,根据勾股定理求出PC,利用面积公式代入求面积即可.
解答  解:如图,当PC⊥AB时,∠OPC取最大值,
解:如图,当PC⊥AB时,∠OPC取最大值,
∵AB是⊙O的直径,AB=6,
∴OA=OP=3,
∵AC=1,
∴OC=2,
在Rt△OCP中,由勾股定理得:CP=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
∴S△OCP=$\frac{1}{2}$OC•PC=$\frac{1}{2}$×2×$\sqrt{5}$=$\sqrt{5}$,
故答案为:$\sqrt{5}$.
点评 本题考查了勾股定理和圆周角定理,本题确定最大值时点P的位置是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.|3.14-π|的计算结果是( )
| A. | 0 | B. | π-3.14 | C. | 3.14-π | D. | -3.14-π |
4.3的相反数是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
3. 如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是( )
如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是( )
 如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是( )
如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是( )| A. | 45° | B. | 55° | C. | 60° | D. | 65° |
 如图,在Rt△ABC中,斜边上的高AD=3,cosB=$\frac{4}{5}$,则AC=$\frac{15}{4}$.
如图,在Rt△ABC中,斜边上的高AD=3,cosB=$\frac{4}{5}$,则AC=$\frac{15}{4}$.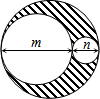 三个圆的位置如图所示,其中m、n分别是两个较小圆的直径,则图中阴影部分的面积为$\frac{1}{2}$mnπ.
三个圆的位置如图所示,其中m、n分别是两个较小圆的直径,则图中阴影部分的面积为$\frac{1}{2}$mnπ.
