题目内容
12．
有理数a、b在数轴上的对应的位置如图所示，则下列各式中正确的是（ ）| A． | a+b＜0 | B． | a+b＞0 | C． | a-b=0 | D． | a-b＞0 |
分析 首先根据数轴确定a，b的符号和大小，再根据有理数的运算法则进行分析判断．
解答 解：由数轴，得a＜0＜b，|a|＞|b|．
A、根据异号两数相加，取绝对值较大的数的符号，则a+b＜0，符合题意；
B、根据异号两数相加，取绝对值较大的数的符号，则a+b＜0，不符合题意；
C、较小的数减去较大的数，则差一定小于0，则a-b＜0，不符合题意；
D、较小的数减去较大的数，则差一定小于0，则a-b＜0，不符合题意．
故选A．
点评 此题考查了运用数轴比较数的大小以及有理数的运算法则，关键是根据数轴确定a，b的符号和大小．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2．
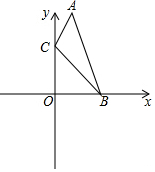如图，在直角坐标系中，点A，B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A，B，C三点不在同一条直线上，当△ABC的周长最小时点C的坐标是（ ）
如图，在直角坐标系中，点A，B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A，B，C三点不在同一条直线上，当△ABC的周长最小时点C的坐标是（ ）| A． | （0，3） | B． | （0，2） | C． | （0，1） | D． | （0，0） |
3．|3.14-π|的计算结果是（ ）
| A． | 0 | B． | π-3.14 | C． | 3.14-π | D． | -3.14-π |
7．如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，图形中M与m、n的关系是（ ）
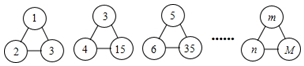
| A． | M=mn | B． | M=m（n+1） | C． | M=mn+1 | D． | M=n（m+1） |
17．下列结论正确的是（ ）
| A． | 分式$\frac{1}{x（x-1）}$有意义的条件是x≠0或x≠1 | |
| B． | $\frac{x-y}{2x+2y}$与$\frac{xy}{{x}^{2}-{y}^{2}}$的最简公分母是2（x-y）（x2-y2） | |
| C． | -0.000 0064用科学记数法表示为-6.4×10-6 | |
| D． | 等式（x2-9）0=1成立的条件是x=±3 |
4．3的相反数是（ ）
| A． | 3 | B． | -3 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{3}$ |
如图，在Rt△ABC中，斜边上的高AD=3，cosB=$\frac{4}{5}$，则AC=$\frac{15}{4}$．
3．
如图，已知AB是△ABC外接圆的直径，∠A=35°，则∠B的度数是（ ）
如图，已知AB是△ABC外接圆的直径，∠A=35°，则∠B的度数是（ ）| A． | 45° | B． | 55° | C． | 60° | D． | 65° |