Question

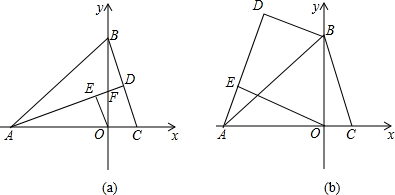
6．如图，直线交坐标轴于A（-3，0），B（0，3）、C（1，0），AD⊥BC于D交y轴于F，OE∥BD．
（1）求F点的坐标；
（2）写出AE、DE、BD三线段的数量关系并证明；
（3）将△ABD沿AB翻折，其他条件不变，（2）中的结论将如何，请证明．

Answer 1

分析 （1）证明△FAO≌△CBO，可知OC=OF，利用点C的坐标即可求出OF的长度，进而求出F的坐标；
（2）利用勾股定理求出AF的长度，然后证明△AOF∽△ADC后可得出DC的长度，再由勾股定理可得AD的长度，然后可证明△AOE∽△ACD，可求出AE的长度，进而求得ED的长度，再由AF=BC，可求得BD的长度；
（3）过点O作OF⊥AB于点F，设AB与OE相交于点G，利用相似可求得FG的长度，进而可求出AG的长度，利用锐角三角函数即可求出AE，进而可求出DE的长度．

解答 解：（1）∵∠AOF=∠BDF=90°，
∠AFO=∠BFD，
∴∠FAO=∠CBO，
∵A（-3，0），B（0，3），
∴OA=OB=3，
在△FAO与△CBO中，
$\left\{\begin{array}{l}{∠AOF=∠BOC}\\{OA=OB}\\{∠FAO=∠CBO}\end{array}\right.$，
∴△FAO≌△CBO（ASA），
∴OF=OC，
∵C（1，0），
∴OC=1；

（2）由勾股定理可求得：AF=$\sqrt{10}$，
∵∠FAO=∠DAC，
∠AOF=∠ADC=90°，
∴△AOF∽△ADC，
∴$\frac{AF}{AC}$=$\frac{OF}{DC}$，
∴DC=$\frac{2\sqrt{10}}{5}$，
∴由勾股定理可求得：AD=$\frac{6\sqrt{10}}{5}$，
∵OF∥BC，
∴△AOE∽△ACD，
∴$\frac{AO}{AC}$=$\frac{AE}{AD}$，
∴AE=$\frac{9\sqrt{10}}{10}$，
∴ED=AE-AE=$\frac{3\sqrt{10}}{10}$，
由（1）可知：AF=BC=$\sqrt{10}$，
∴BD=BC-DC=$\frac{3\sqrt{10}}{5}$，
∴AE=$\frac{3}{4}$（BD+DE）；

（3）过点O作OF⊥AB于点F，设AB与OE相交于点G，
由（2）可知：AD=$\frac{6\sqrt{10}}{5}$，BD=$\frac{3\sqrt{10}}{5}$，
∴tan∠DAB=$\frac{BD}{AD}$=$\frac{1}{2}$，
∵OA=OB=3，
∴∠BAO=45°，
∴AF=OF=$\frac{3\sqrt{2}}{2}$，
∵∠DAB=∠GOF，
∴tan∠GOF=$\frac{1}{2}$，
∴$\frac{GF}{OF}=\frac{1}{2}$，
∴GF=$\frac{3\sqrt{2}}{4}$，
∴AG=AF-GF=$\frac{3\sqrt{2}}{4}$，
∵tan∠DAB=$\frac{1}{2}$，
∴cos∠DAB=$\frac{2\sqrt{5}}{5}$，
∴$\frac{AE}{AG}$=$\frac{2\sqrt{5}}{5}$，
∴AE=$\frac{3\sqrt{10}}{10}$，
∴DE=AD-AE=$\frac{9\sqrt{10}}{10}$，
∴DE=$\frac{1}{2}$（AD+BD）．

点评 本题考查几何变换综合题，涉及勾股定理，相似三角形判定与性质，全等三角形判定与性质，锐角三角函数等知识，综合程度较高，需要学生灵活运用所学知识．