题目内容
8.若反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象过点(3,-4),则下列各点中也在该图象上的点是( )| A. | (2,6) | B. | (-6,-2) | C. | (-3,4) | D. | (-3,-4) |
分析 根据反比例函数图象上点的坐标特征易得k=-12,然后再反比例函数图象上点的坐标特征对四个点进行判断.
解答 解:∵反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象过点(3,-4),
∴k=3×(-4)=-12,
而2×6=-6×(-2)=-3×(-4)=12,-3×4=-12,
∴点(-3,4)在函数y=-$\frac{12}{x}$的图象上.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若x-y=2,x-z=3,则(y-z)2-3(z-y)+9的值为( )
| A. | 13 | B. | 11 | C. | 5 | D. | 7 |
16.设$\sqrt{7}$的小数部分是a,则(4+a)•a的值为( )
| A. | 1 | B. | $\sqrt{7}$ | C. | 3 | D. | $\sqrt{7}$-2 |
20.若A(2x-5,6-2x)在第四象限,则x的取值范围是( )
| A. | x>3 | B. | x>-3 | C. | x<-3 | D. | x<3 |
17.在求1+6+62+63+64+65+66+67+68+69的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:
S=1+6+62+63+64+65+66+67+68+69①然后在①式的两边都乘以6,得:
6S=6+62+63+64+65+66+67+68+69+610②
②-①得6S-S=610-1,即5S=610-1,所以S=$\frac{{6}^{10}-1}{5}$,得出答案后,爱动脑筋的小林想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2014的值?你的答案是( )
S=1+6+62+63+64+65+66+67+68+69①然后在①式的两边都乘以6,得:
6S=6+62+63+64+65+66+67+68+69+610②
②-①得6S-S=610-1,即5S=610-1,所以S=$\frac{{6}^{10}-1}{5}$,得出答案后,爱动脑筋的小林想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2014的值?你的答案是( )
| A. | $\frac{{a}^{2014}-1}{a-1}$ | B. | $\frac{{a}^{2015}-1}{a-1}$ | C. | $\frac{{a}^{2014}-1}{a}$ | D. | a2014-1 |
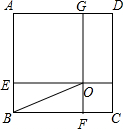 如图,在正方形ABCD中,点E、F、G、H分别在四边上,EH∥BC,GF∥AB,EH与FG交于点O,且AE=AG,若AE比CH长2,△BOF的面积为$\frac{3}{2}$
如图,在正方形ABCD中,点E、F、G、H分别在四边上,EH∥BC,GF∥AB,EH与FG交于点O,且AE=AG,若AE比CH长2,△BOF的面积为$\frac{3}{2}$