题目内容

18．已知非零实数a，b满足a2+ab+b2+a-b+1=0，则$\frac{1}{a}$+$\frac{1}{b}$的值等于（　　）
A．-1B．0C．1D．2

分析 由a2+ab+b2+a-b+1=0，两边乘2，进一步利用完全平方公式分组分解，进一步利用非负数的性质得出a、b的数值，代入求得答案即可．

解答 解：∵a2+ab+b2+a-b+1=0，
∴2a2+2ab+2b2+2a-2b+2=0，
∴（a2+2ab+b2）+（a2+2a+1）+（b2-2b+1）=0，
∴（a+b）2+（a+1）2+（b-1）2=0，
∴a+b=0，a+1=0，b-1=0，
解得a=-1，b=1，
∴$\frac{1}{a}$+$\frac{1}{b}$=0．
故选：B．

点评 此题考查配方法的运用，以及非负数的性质，掌握完全平方公式是解决问题的关键．

练习册系列答案
相关题目
8．计算：
（1）4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
（2）（-2$\sqrt{12}$）2÷（$\sqrt{75}$+3$\sqrt{\frac{1}{3}}$-$\sqrt{48}$）
9．已知am=5，an=2，则am+n的值等于（　　）
A．25B．10C．8D．7
6．（1）$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
（2）先化简，再求值：$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$÷（$\frac{1}{a}$-$\frac{1}{b}$），其中a=$\sqrt{2}$+1，b=$\sqrt{2}$-1．
13．若一个多边形的内角和为360°，则这个多边形的边数为4．
3．计算：
（1）$\frac{1}{2}$$\sqrt{3}$÷$\sqrt{\frac{1}{12}}$×$\sqrt{27}$；
（2）$\frac{\sqrt{12}×\sqrt{6}}{\sqrt{8}}$；
（3）6$\sqrt{15}$÷3$\sqrt{\frac{1}{5}}$×$\sqrt{2\frac{2}{3}}$．
10．（1）平面内有n条直线，其中没有两条平行，也没有三条交于一点，共有多少个交点？
（2）空间内有n个平面，其中没有两个互相平行，也没有三个交于一条直线，一共有多少条交线？
7．某一时刻身高1.6m的小亮在太阳光下的影长为2m，同时测得学校旗杆的影长是15m，那么这根旗杆的高度是12m．
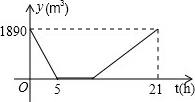8．某游泳池内现存水1890立方米，已知该游泳池的防水速度是进水速度的2倍，假设在换水时需要经历“放水→清洗→进水”的过程，其中游泳池内剩余的水量y（m3）与换水时间t（h）之间的函数关系如图所示．试根据图象解答下列问题：
（1）求进水的速度及清洗该游泳池所用的时间；
（2）求进水过程中的y（m3）与换水时间t（h）之间的函数关系式，并求在整个换水过程中，当游泳池中的水量为1512m3时的换水时间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网