题目内容
6.(1)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$(2)先化简,再求值:$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$÷($\frac{1}{a}$-$\frac{1}{b}$),其中a=$\sqrt{2}$+1,b=$\sqrt{2}$-1.
分析 (1)先将二次根式化简,然后进行加减;
(2)先将括号内的部分相减,因式分解后约分即可.
解答 (1)解:原式=4-$\sqrt{6}$+2$\sqrt{6}$=4+$\sqrt{6}$;
(2)解:原式=$\frac{(a-b)^{2}}{(a+b)(a-b)}$÷$\frac{b-a}{ab}$
=$\frac{{(a-b)}^{2}}{(a+b)(a-b)}$•$\frac{ab}{b-a}$
=-$\frac{ab}{a+b}$,
当a=$\sqrt{2}$+1,b=$\sqrt{2}$-1时,原式=-$\frac{\sqrt{2}}{4}$.
点评 (1)本题考查了二次根式的混合运算,熟悉二次根式的化简是解题的关键;
(2)本题考查了分式的化简求值,熟悉因式分解是解题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
16.若xa+2+yb-1+3=0是关于x,y的二元一次方程,则a、b的值为( )
| A. | a=-1,b=2 | B. | a=-1,b=1 | C. | a=1,b=1 | D. | a=1,b=2 |
11.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (-2x)3=-2x3 | ||
| C. | $\sqrt{2}+\sqrt{8}=3\sqrt{2}$ | D. | (a-b)(-a+b)=-a2-2ab-b2 |
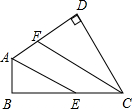 如图,已知在四边形ABCD中,AE、CF分别是∠DAB及∠DCB的平分线,∠B=∠D=90°,求证:AE∥CF.
如图,已知在四边形ABCD中,AE、CF分别是∠DAB及∠DCB的平分线,∠B=∠D=90°,求证:AE∥CF. 如图,在锐角三角形ABC中,AD⊥BC于D,E、F、G分别是AC、AB、BC的中点.求证:FG=DE.
如图,在锐角三角形ABC中,AD⊥BC于D,E、F、G分别是AC、AB、BC的中点.求证:FG=DE.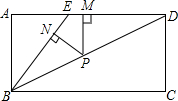 如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.
如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.