题目内容
2.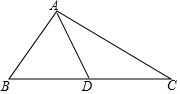 如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=$\frac{11}{10}$,则tan∠BAD=$\frac{33}{10}$.
如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=$\frac{11}{10}$,则tan∠BAD=$\frac{33}{10}$.
分析 延长AD到E使AD=DE,根据全等三角形的性质得到∠B=∠DCE,∠BAD=∠CED,推出△AEC是等腰三角形,过A作CF⊥EC,过D作CH⊥EC,根据平行线分线段成比例定理即可得到结论.
解答  解:延长AD到E使AD=DE,
解:延长AD到E使AD=DE,
在△ADB与△ECD中,$\left\{\begin{array}{l}{BD=CD}\\{∠ADB=∠CDE}\\{AD=DE}\end{array}\right.$,
∴△ABD≌△ECD,
∴∠B=∠DCE,∠BAD=∠CED,
∵∠BAD=∠B+∠ACB=∠ACB+∠DCE=∠ACE,
∴∠E=∠ACE,
∴△AEC是等腰三角形,
过A作CF⊥EC,过D作CH⊥EC,
设DH=11,HC=10,EH=x,
则$\frac{DH}{AF}$=$\frac{EH}{EF}$,
∴$\frac{11}{22}$=$\frac{x}{\frac{10+x}{2}}$,
∴x=$\frac{10}{3}$,
∴tan∠BAD=tan∠DEC=$\frac{11}{\frac{10}{3}}$=$\frac{33}{10}$.
故答案为:$\frac{33}{10}$.
点评 本题考查了解直角三角形,全等三角形的判定和性质,等腰三角形的判定和性质,平行线分线段成比例定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
13.在直角坐标系中,O为原点,A(0,4),点B在直线y=kx+6(k>0)上,若以O、A、B为顶点所作的直角三角形有且只有三个时,k的值为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 3 | D. | $\frac{3}{2}$ |
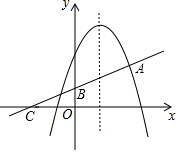 如图,顶点为(1,4)的抛物线y=ax2+bx+c与直线y=$\frac{1}{2}$x+n交于点A(2,2),直线y=$\frac{1}{2}$x+n与y轴交于点B与x轴交于点C
如图,顶点为(1,4)的抛物线y=ax2+bx+c与直线y=$\frac{1}{2}$x+n交于点A(2,2),直线y=$\frac{1}{2}$x+n与y轴交于点B与x轴交于点C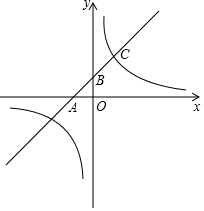 已知:如图,一次函数y=kx+b的图象与x轴负半轴相交于点A,与y正半轴相交于点B,与反比例函数y=$\frac{m}{x}$图象的一个交点为C(2,4),且 AB=BC.
已知:如图,一次函数y=kx+b的图象与x轴负半轴相交于点A,与y正半轴相交于点B,与反比例函数y=$\frac{m}{x}$图象的一个交点为C(2,4),且 AB=BC. 如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.
如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.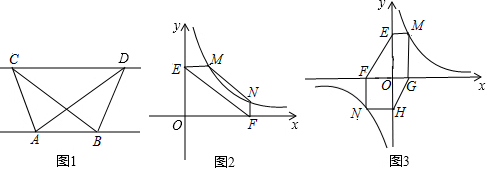
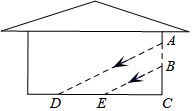 如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=2.5 米.
如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=2.5 米.