题目内容
14．已知$\sqrt{x-2}$+$\sqrt{8-x}$有意义，则|2-x|+|x-8|=6．分析 直接利用二次根式有意义的条件得出x的取值范围，再利用绝对值的性质化简求出答案．
解答 解：∵$\sqrt{x-2}$+$\sqrt{8-x}$有意义，
∴$\left\{\begin{array}{l}{x-2≥0}\\{8-x≥0}\end{array}\right.$，
解得：2≤x≤8，
∴|2-x|+|x-8|=x-2+8-x=6．
故答案为：6．
点评 此题主要考查了二次根式有意义的条件以及绝对值的性质，正确得出x的取值范围是解题关键．
练习册系列答案
相关题目
如图，已知四边形ABCD为⊙O的内接四边形，AE是⊙O的直径，连接BE、BD，P为⊙O外一点，连接PA，若∠AEB=40°，AE=12．
如图，在△ABC中，∠B=38°，∠C=40°，AB的垂直平分线交BC于D，AC的垂直平分线交BC于E，则∠DAE=24°．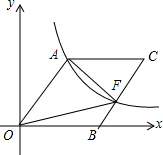
如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB=$\frac{4}{5}$，反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A，与BC交于点F，则△AOF的面积等于40．
如图，OC是∠AOB内部的一条射线，且OM，ON分别平分∠AOC与∠BOC．