题目内容
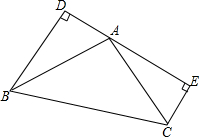 如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4,求AB2的值.
如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4,求AB2的值.考点:全等三角形的判定与性质,勾股定理
专题:
分析:根据SAS,可得△ABD与△CEA的关系,根据全等三角形的性质,可得∠CAE与∠ABD的关系,根据直角三角形的性质,可得∠ABD与∠BAD的关系,根据余角的性质,可得∠CAE与∠BAD的关系,根据平角的关系,可得∠BAC的度数,根据勾股定理,可得答案.
解答:解:BD⊥DE于D,CE⊥DE于E,
∠D=∠E=90°.
在△ABD与△CEA中
,
∴△ABD≌△CEA(SAS),
∴∠CAE=∠ABD,AB=AE.
∵∠ABD+∠BAD=90°,
∴∠CAE+∠BAD=90°,
∴∠BAC=90°.
在Rt△ABD中,由勾股定理得
AB=
=2
,
在Rt△ABC中,由勾股定理得
BC2=AB2+AC2=20=20=40.
∠D=∠E=90°.
在△ABD与△CEA中
|
∴△ABD≌△CEA(SAS),
∴∠CAE=∠ABD,AB=AE.
∵∠ABD+∠BAD=90°,
∴∠CAE+∠BAD=90°,
∴∠BAC=90°.
在Rt△ABD中,由勾股定理得
AB=
| AD2+BD2 |
| 5 |
在Rt△ABC中,由勾股定理得
BC2=AB2+AC2=20=20=40.
点评:本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,勾股定理.

练习册系列答案
相关题目
下列各对数中,互为相反数的有( )
(-1)与+(-1),+(+1)与-1,-(-2)与+(-2),+[-(+1)]与-[+(-1)],-(+2)与-(-2),-(-
)与+(+
).
(-1)与+(-1),+(+1)与-1,-(-2)与+(-2),+[-(+1)]与-[+(-1)],-(+2)与-(-2),-(-
| 1 |
| 3 |
| 1 |
| 3 |
| A、6对 | B、5对 | C、4对 | D、3对 |
 如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )
如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )| A、45 | B、50 | C、60 | D、90 |
 如图,在直角坐标系中,一次函数y=kx+b的图形与反比例函数y=
如图,在直角坐标系中,一次函数y=kx+b的图形与反比例函数y= 如图所示,一座拱桥的纵截面是抛物线的一段,已知拱桥的跨度是8米,水面宽6米时,水深3.5米,若水面宽5米,水有多深?
如图所示,一座拱桥的纵截面是抛物线的一段,已知拱桥的跨度是8米,水面宽6米时,水深3.5米,若水面宽5米,水有多深?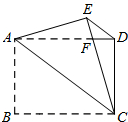 如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F,若AB=4,BC=6,求△FAC的周长和面积.
如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F,若AB=4,BC=6,求△FAC的周长和面积.