题目内容
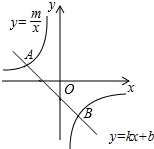 如图,在直角坐标系中,一次函数y=kx+b的图形与反比例函数y=
如图,在直角坐标系中,一次函数y=kx+b的图形与反比例函数y=| m |
| x |
A(-2,1),B(1,n)两点.
(1)求上述反比例函数和一次函数的表达式;
(2)在x轴上是否存在点P,使S△APB=2S△AOB?若存在,求出点P的坐标;若不存在,说明理由.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)将A坐标代入反比例解析式求出m的值,确定出反比例解析式,将B坐标代入反比例解析式求n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)设一次函数与x轴交于C点,求出C坐标,确定出OC的长,三角形AOB面积=三角形AOC面积+三角形BOC面积,根据S△APB=2S△AOB,即可求得PC的长,进而求得P的坐标.
(2)设一次函数与x轴交于C点,求出C坐标,确定出OC的长,三角形AOB面积=三角形AOC面积+三角形BOC面积,根据S△APB=2S△AOB,即可求得PC的长,进而求得P的坐标.
解答:解:(1)将A(-2,1)代入反比例解析式得:m=-2,
则反比例解析式为y=-
;
将B(1,n)代入反比例解析式得:n=-2,即B(1,-2),
将A与B坐标代入y=kx+b中,得:
,
解得:
,
则一次函数解析式为y=-x-1;
(2)连接OA,OB,设一次函数与x轴交于点C,
对于一次函数y=-x-1,令y=0,得到x=-1,即OC=1,
∴C(-1,0),
则S△AOB=S△AOC+S△BOC=
×1×1+
×1×2=1.5.
∴S△APB=S△APC+S△BPC=
PC×1+
PC×2=
+PC=
,
∵S△APB=2S△AOB
∴3=
,
解得PC=2,
∴P(1,0)或P(-3,0).
所以P的坐标为(1,0),(-3,0).
则反比例解析式为y=-
| 2 |
| x |
将B(1,n)代入反比例解析式得:n=-2,即B(1,-2),

将A与B坐标代入y=kx+b中,得:
|
解得:
|
则一次函数解析式为y=-x-1;
(2)连接OA,OB,设一次函数与x轴交于点C,
对于一次函数y=-x-1,令y=0,得到x=-1,即OC=1,
∴C(-1,0),
则S△AOB=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△APB=S△APC+S△BPC=
| 1 |
| 2 |
| 1 |
| 2 |
| PC |
| 2 |
| 3PC |
| 2 |
∵S△APB=2S△AOB
∴3=
| 3PC |
| 2 |
解得PC=2,
∴P(1,0)或P(-3,0).
所以P的坐标为(1,0),(-3,0).
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
 反比例函数y=
反比例函数y=| k |
| x |
| A、1 | B、2 | C、3 | D、4 |
在Rt△ABC中,∠C=90°,AC=5,BC=12,则其外接圆半径为( )
| A、5 | B、12 | C、13 | D、6.5 |
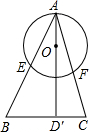 已知AD是⊙O的直径,AD′⊥BC,AB、AC分别与圆相交于E、F,那么下列等式中一定成立的是( )
已知AD是⊙O的直径,AD′⊥BC,AB、AC分别与圆相交于E、F,那么下列等式中一定成立的是( )| A、AE•BF=AF•CF |
| B、AE•AB=AO•AD′ |
| C、AE•AB=AF•AC |
| D、AE•AF=AO•AD |
某人以8折优惠价买一套服装,省了25元.买这套服装实际用了( )
| A、100元 | B、125元 |
| C、25元 | D、31.25元 |
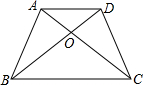 如图,在四边形ABCD中,AC与BD相交于点O,如果△ABO≌△DCO,试在图中再找出一对全等三角形,并加以证明.
如图,在四边形ABCD中,AC与BD相交于点O,如果△ABO≌△DCO,试在图中再找出一对全等三角形,并加以证明.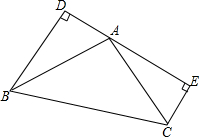 如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4,求AB2的值.
如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4,求AB2的值.