题目内容
 如图所示,一座拱桥的纵截面是抛物线的一段,已知拱桥的跨度是8米,水面宽6米时,水深3.5米,若水面宽5米,水有多深?
如图所示,一座拱桥的纵截面是抛物线的一段,已知拱桥的跨度是8米,水面宽6米时,水深3.5米,若水面宽5米,水有多深?考点:二次函数的应用
专题:应用题
分析:以跨度所在的水平线为x轴,以抛物线的对称轴为y轴建立直角坐标系,则根据题中数据得到B(4,0),D(3,3.5),再利用待定系数法确定抛物线的解析式为y=-0.5x2+8,然后求自变量为2.5所对应的函数值即可.
解答:解: 建立如图所示的直角坐标系,AB=8m,CD=6m,EF=5m,OH=3.5m,
建立如图所示的直角坐标系,AB=8m,CD=6m,EF=5m,OH=3.5m,
则B(4,0),D(3,3.5),
设抛物线的解析式为y=ax2+c,
把B(4,0),D(3,3.5)代入得
,
解得
.
所以抛物线的解析式为y=-0.5x2+8,
当x=
时,y=-0.5x2+8=-0.5×
+8=4.875,
所以F点坐标为(2.5,4.875),
所以水面宽5米,水有4.875m深.
 建立如图所示的直角坐标系,AB=8m,CD=6m,EF=5m,OH=3.5m,
建立如图所示的直角坐标系,AB=8m,CD=6m,EF=5m,OH=3.5m,则B(4,0),D(3,3.5),
设抛物线的解析式为y=ax2+c,
把B(4,0),D(3,3.5)代入得
|
解得
|
所以抛物线的解析式为y=-0.5x2+8,
当x=
| 5 |
| 2 |
| 25 |
| 4 |
所以F点坐标为(2.5,4.875),
所以水面宽5米,水有4.875m深.
点评:本题考查了二次函数的应用:构建二次函数模型解决实际问题,用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.

练习册系列答案
相关题目
 取一张长方形纸片,按图中所示的方法折叠一角,得到折痕EF,若∠BEF=54°,则∠BFC等于( )
取一张长方形纸片,按图中所示的方法折叠一角,得到折痕EF,若∠BEF=54°,则∠BFC等于( )| A、100° | B、108° |
| C、118° | D、120° |
 如图,直线a、b相交形成四个角,下列说法错误的是( )
如图,直线a、b相交形成四个角,下列说法错误的是( )| A、∠1与∠2互为邻补角 |
| B、∠1与∠3互为对顶角 |
| C、∠3与∠4互为邻补角 |
| D、∠3与∠2互为对顶角 |
某人以8折优惠价买一套服装,省了25元.买这套服装实际用了( )
| A、100元 | B、125元 |
| C、25元 | D、31.25元 |
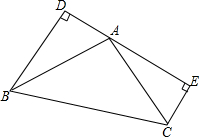 如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4,求AB2的值.
如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4,求AB2的值.