题目内容
11.阅读理解:学习了三角形全等的判定方法:“SAS”,“ASA”,“AAS”,“SSS”和直角三角形全等的判定方法“HL”后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA”的情形进行研究.
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D.
初步探究:
如图1,已知AC=DF,∠A=∠D,过C作CH⊥射线AM于点H,对△ABC 的CB边进行分类,可分为“CB<CH,CB=CH,CH<CB<CA,”三种情况进行探究.

深入探究:
第一种情况,当BC<CH时,不能构成△ABC和△DEF.
第二种情况,(1)如图2,当BC=CH时,在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D,根据HL或AAS,可以知道Rt△ABC≌Rt△DEF.

第三种情况,(2)当CH<BC<CA时,△ABC和△DEF不一定全等.请你用尺规在图1的两个图形中分别补全△ABC和△DEF,使△DEF和△ABC不全等(表明字母,不写作法,保留作图痕迹).
(3)从上述三种情况发现,只有当BC=CH时,才一定能使△ABC≌△DEF. 除了上述三种情况外,BC边还可以满足什么条件,也一定能使△ABC≌△DEF?写出结论,并利用备用图证明.

分析 (1)根据 HL或AAS,可以知道Rt△ABC≌Rt△DEF;
(2)如图1所示:以C或F为圆心,BC的长为半径画弧,分别交AM,DN与B,E,则△ABC与△DEF不全等;
(3)当BC≥CA时,也能使△ABC≌△DEF,①当BC=CA时,△ABC和△DEF是有一个底角相等的等腰三角形,根据AAS易证两三角形全等,②当BC>CA时,在射线AM上取点B,使BC>CA,连接BC,以F为圆心,CB长为半径画弧交射线DN于点E,连接FE,则BC=EF,过点F作FG⊥DE于点G,证明△CAH≌△FDG(AAS),得到CH=FG,通过Rt△CBH≌Rt△FEG(HL),得到∠CBA=∠FED,证得△ABC≌△DEF(AAS).
解答 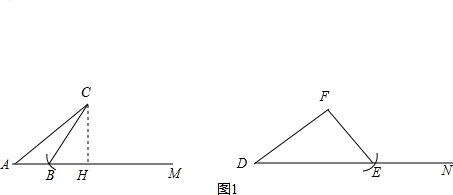 解:(1)解:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D,根据 HL或(AAS),可以知道Rt△ABC≌Rt△DEF.
解:(1)解:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D,根据 HL或(AAS),可以知道Rt△ABC≌Rt△DEF.
故答案为;HL或AAS;
(2)如图1所示:
(3)当BC≥CA时,也能使△ABC≌△DEF,
证明:①当BC=CA时,△ABC和△DEF是有一个底角相等的等腰三角形,
根据AAS易证两三角形全等,
②当BC>CA时,在射线AM上取点B,使BC>CA,连接BC,
以F为圆心,CB长为半径画弧交射线DN于点E,连接FE,则BC=EF,
过点F作FG⊥DE于点G,
在△CAH和△FDG中,$\left\{\begin{array}{l}{∠A=∠D}\\{∠AHC=∠DGF}\\{AC=DF}\end{array}\right.$,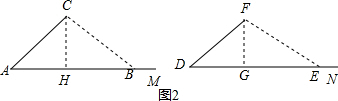
∴△CAH≌△FDG(AAS),
∴CH=FG,
在Rt△CBH和Rt△FEG中,$\left\{\begin{array}{l}CH=FG\\ CB=FE\end{array}\right.$
∴Rt△CBH≌Rt△FEG(HL),
∴∠CBA=∠FED,
在△ABC和△EFD中,$\begin{array}{l}\left\{\begin{array}{l}∠CBA=∠FED\\∠A=∠D\\ AC=DF\end{array}\right.\end{array}$
∴△ABC≌△DEF(AAS).
点评 本题考查了全等三角形的判定与性质,应用与设计作图,熟练掌握三角形全等的判定方法是解题的关键,阅读量较大,审题要认真仔细.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案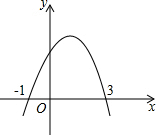 如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,则下列判断中,正确的是( )
如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,则下列判断中,正确的是( )①图象的对称轴是直线x=1;
②当x>1时,y随x的增大而减小;
③一元二次方程ax2+bx+c=0的两个根是-1和3;
④当-1<x<3时,y<0.
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ④ |
| A. | -1 | B. | 1 | C. | 3 | D. | -3 |
 周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题:
周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题:
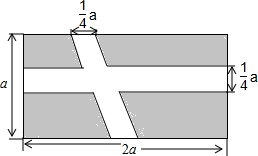 小林负责一块宽为a,长为2a的长方形草坪铺设鹅卵石小路供游人行走,他计划铺设两条宽为$\frac{1}{4}$a的鹅卵石(如图所示),其余部分全部种草
小林负责一块宽为a,长为2a的长方形草坪铺设鹅卵石小路供游人行走,他计划铺设两条宽为$\frac{1}{4}$a的鹅卵石(如图所示),其余部分全部种草