Question

1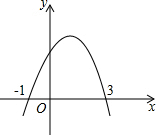．如图，抛物线y=ax²+bx+c交x轴于（-1，0）、（3，0）两点，则下列判断中，正确的是（　　）
①图象的对称轴是直线x=1；
②当x＞1时，y随x的增大而减小；
③一元二次方程ax²+bx+c=0的两个根是-1和3；
④当-1＜x＜3时，y＜0．

• A． ①②
• B． ①②④
• C． ①②③
• D． ④

Answer 1

分析 由抛物线与x轴的两个交点的横坐标即可求出对称轴，得出①正确；
由图象得出a＜0，根据二次函数的性质即可得出②正确；
抛物线y=ax²+bx+c与x轴的两个交点横坐标得出③正确；
根据图象得出④错误．

解答 解：∵抛物线y=ax²+bx+c交x轴于（-1，0）、（3，0）两点，
∴对称轴为：x=$\frac{-1+3}{2}$=1，
∴①正确；
由图象得：a＜0，
∴当x＞1时，y随x的增大而减小；
∴②正确；
∵抛物线y=ax²+bx+c交x轴于（-1，0）、（3，0）两点，
即y=0时，x=-1，或x=3，
∴一元二次方程ax²+bx+c=0的两个根是-1和3；
∴③正确；
由图象得：当-1＜x＜3时，y＞0，
∴④错误；
综上所述：正确的结论是①②③．
故选：C．

点评 本题考查了抛物线与x轴的交点、对称轴的求法、二次函数的图象与性质、二次函数与一元二次方程的关系；熟练掌握二次函数的图象与性质是解决问题的关键．