题目内容
1．
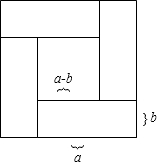用四个相同的长方形与一个小正方形无重叠、无缝隙地拼成一个大正方形的图案（如图），则由图形能得出（a-b）2=（a+b）2-4ab（化为a、b两数和与积的形式）
分析 根据图形先求出小正方形的边长即可得到面积，或者先求出大正方形的面积，然后再减去四个长方形的面积；根据同一个小正方形的面积，利用两种不同的求法即可得到等式．
解答 解：∵小正方形的边长为：（a-b），
∴面积为（a-b）2，
又∵小正方形的面积=大正方形的面积-4×长方形的面积，
∴小正方形面积为：（a-b）2=（a+b）2-4ab，
答案为：（a+b）2-4ab．
点评 本题考查了完全平方公式的几何解释，根据同一个图形的面积利用不同的方法求解，结果相等解答即可，难度不大．
练习册系列答案
相关题目
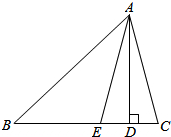如图，AD是△ABC的BC边上的高，AE平分∠BAC，若∠B=42°，∠C=70°，求∠AEC和∠DAE的度数．
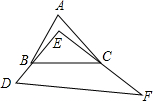将如图所示的一块直角三角板放置在△ABC上，使三角板的两条直角边DE、EF分别经过点B、C，若∠A=65°，则∠ABE+∠ACE=25°．
11．下列运算正确的是（ ）
| A． | $\sqrt{4}=±2$ | B． | |-2|=-2 | C． | -22=4 | D． | $-\sqrt{4}=-2$ |