题目内容
2.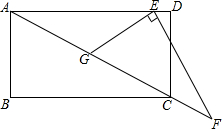 如图,矩形ABCD中,AB=6,∠ACB=30°,Rt△EFG中,∠E=90°,EG=5,GF=10,点E在AD上时,将Rt△EFG绕点C顺时针旋转α(0<α<90°)得到E1F1G1.设直线E1F1交直线AD于点M,直线E1F1交直线AC于点N,当AM=AN时,求MA的值.
如图,矩形ABCD中,AB=6,∠ACB=30°,Rt△EFG中,∠E=90°,EG=5,GF=10,点E在AD上时,将Rt△EFG绕点C顺时针旋转α(0<α<90°)得到E1F1G1.设直线E1F1交直线AD于点M,直线E1F1交直线AC于点N,当AM=AN时,求MA的值.
分析 如图,作CH⊥MN于H,首先求出CF的长,再证明∠HCN=15°,在图1中,取CK=KN,设CK=KN=x,列出方程求出x,再利用勾股定理求出CN即可解决问题.
解答 解:如图,作CH⊥MN于H,
∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,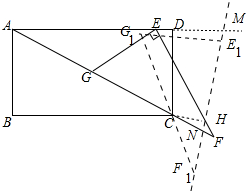
∴∠ACB=∠CAD=30°,
在RT△ABC中,∵∠B=90°,∠ACB=30°,AB=6,
∴AC=2AB=12,
在RT△EGF中,∵∠GEF=90°,EG=5,GF=10,
∴GF=2EG,
∴∠EFG=30°,∠EGF=60°,
∵∠EGF=∠CAD+∠AEG,
∴∠GAE=∠GEA=30°,
∴GA=GE=5,GC=7,CF=3,
在RT△CHF1中,∵∠CHF1=90°,CF1=3,∠F1=30°,
∴CH=$\frac{1}{2}$CF1=$\frac{3}{2}$,
在RT△CHN中,∵∠CNH=∠AMN=$\frac{1}{2}(180°-30°)$=75°,
∴∠HCN=15°,
如图1中,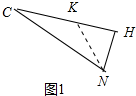 在RT△CHN中,取CK=KN,设CK=KN=x,
在RT△CHN中,取CK=KN,设CK=KN=x,
∴∠KCN=∠KNC=15°,
∴∠HKN=30°,
∴HN=$\frac{1}{2}$x,KH=$\frac{\sqrt{3}}{2}$x,
∴CK+KH=CH,
∴x+$\frac{\sqrt{3}}{2}$x=$\frac{3}{2}$,
∴x=6-3$\sqrt{3}$,
∴CN=$\sqrt{C{H}^{2}+N{H}^{2}}$=$\sqrt{(\frac{3}{2})^{2}+(\frac{6-3\sqrt{3}}{2})^{2}}$=$\frac{3}{2}$($\sqrt{6}$-$\sqrt{2}$).
∴AM=AN=AC+CN=12+$\frac{3}{2}$($\sqrt{6}$-$\sqrt{2}$)=12+$\frac{3}{2}$$\sqrt{6}$-$\frac{3}{2}$$\sqrt{2}$.
点评 本题考查矩形的性质、旋转变换、勾股定理、等腰三角形的判定和性质等知识,解题的关键是正确画出图形,发现∠HCN=15°是解题的突破口,学会添加辅助线把15°转化为30°,学会利用方程的思想解决问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | x>0 | B. | x≥2 | C. | x≥-2 | D. | x≤2 |
 如图,在菱形ABCD中,下列结论中错误的是( )
如图,在菱形ABCD中,下列结论中错误的是( )| A. | ∠1=∠2 | B. | AC⊥BD | C. | AB=AD | D. | AC═BD |
| A. | 6 | B. | 12 | C. | 24 | D. | 30 |
 如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为30.
如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为30.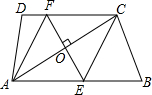 如图,在四边形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB,CD于点E,F,连接CE,AF.
如图,在四边形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB,CD于点E,F,连接CE,AF.