题目内容
20.已知关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+y=1+2m}\\{x+2y=2-m}\end{array}\right.$的解满足不等式组$\left\{\begin{array}{l}{x-y<8}\\{x+y>1}\end{array}\right.$,则m的取值范围是什么?分析 将方程组两方程相加减可得x+y、x-y,代入不等式组可得关于m的不等式组,求解可得.
解答 解:在方程组$\left\{\begin{array}{l}{2x+y=1+2m}&{①}\\{x+2y=2-m}&{②}\end{array}\right.$中,
①+②,得:3x+3y=3+m,即x+y=$\frac{3+m}{3}$,
①-②,得:x-y=-1+3m,
∵$\left\{\begin{array}{l}{x-y<8}\\{x+y>1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{3m-1<8}\\{\frac{3+m}{3}>1}\end{array}\right.$,
解得:0<m<3.
点评 本题主要考查解二元一次方程组和一元一次不等式组的能力,根据题意得出关于m的不等式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.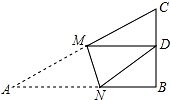 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )| A. | 4 | B. | 5 | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
 解不等式$\frac{2x-1}{3}-\frac{9x+2}{6}≤1$,把它的解集在数轴上表示出来,并求出这个不等式的负整数解.
解不等式$\frac{2x-1}{3}-\frac{9x+2}{6}≤1$,把它的解集在数轴上表示出来,并求出这个不等式的负整数解. 如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( ) 如图,矩形ABCD中,AB=6,∠ACB=30°,Rt△EFG中,∠E=90°,EG=5,GF=10,点E在AD上时,将Rt△EFG绕点C顺时针旋转α(0<α<90°)得到E1F1G1.设直线E1F1交直线AD于点M,直线E1F1交直线AC于点N,当AM=AN时,求MA的值.
如图,矩形ABCD中,AB=6,∠ACB=30°,Rt△EFG中,∠E=90°,EG=5,GF=10,点E在AD上时,将Rt△EFG绕点C顺时针旋转α(0<α<90°)得到E1F1G1.设直线E1F1交直线AD于点M,直线E1F1交直线AC于点N,当AM=AN时,求MA的值.