题目内容
12.一个直角三角形的周长是12,斜边长为5,则其面积为( )| A. | 6 | B. | 12 | C. | 24 | D. | 30 |
分析 设一直角边长为x,另一直角边长为y,根据三角形的周长以及面积即可求出两直角边的乘积,进而得到答案.
解答 解:设一直角边长为x,另一直角边长为y,
由题意可得直角三角形的周长为12,斜边长为5,则可知两直角边长和为7,
直角三角形面积为两直角边乘积的一半,根据勾股定理可得一直角边长2+另一直角边长2=斜边长2.
联立$\left\{\begin{array}{l}{x+y+5=12}\\{{x}^{2}+{y}^{2}=25}\end{array}\right.$,将x+y=7两边同时平方,即可求得xy=12,
面积S=$\frac{1}{2}$×一直角边长×另一直角边长=$\frac{1}{2}$xy=6,
故选:A.
点评 此题主要考查了勾股定理以及完全平方公式的应用,熟练应用完全平方公式是解题关键.

练习册系列答案
相关题目
7.已知$\left\{\begin{array}{l}{3x+2t=4}\\{2y-t=3}\end{array}\right.$,则用含x的代数式表示y为y=$\frac{-3x+10}{4}$.
1. 如图,在平面直角坐标系中,将点A(-2,3)向右平移3个长度单位,那么平移后对应的点A′的坐标是( )
如图,在平面直角坐标系中,将点A(-2,3)向右平移3个长度单位,那么平移后对应的点A′的坐标是( )
 如图,在平面直角坐标系中,将点A(-2,3)向右平移3个长度单位,那么平移后对应的点A′的坐标是( )
如图,在平面直角坐标系中,将点A(-2,3)向右平移3个长度单位,那么平移后对应的点A′的坐标是( )| A. | (-2,-3) | B. | (-2,6) | C. | (1,3) | D. | (-2,1) |
2.下列计算中,不正确的是( )
| A. | -2x+3x=x | B. | 2xy2•(-x)=-2x2y2 | C. | (-2x2y)3=-6x2y3 | D. | 6xy2÷2xy=3y |
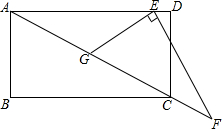 如图,矩形ABCD中,AB=6,∠ACB=30°,Rt△EFG中,∠E=90°,EG=5,GF=10,点E在AD上时,将Rt△EFG绕点C顺时针旋转α(0<α<90°)得到E1F1G1.设直线E1F1交直线AD于点M,直线E1F1交直线AC于点N,当AM=AN时,求MA的值.
如图,矩形ABCD中,AB=6,∠ACB=30°,Rt△EFG中,∠E=90°,EG=5,GF=10,点E在AD上时,将Rt△EFG绕点C顺时针旋转α(0<α<90°)得到E1F1G1.设直线E1F1交直线AD于点M,直线E1F1交直线AC于点N,当AM=AN时,求MA的值.
 如图,在菱形ABCD中,AB=6,∠ABC=60°,动点E、F同时从点B出发,其中点E从点B向点A以每秒1个单位的速度运动,点F从点B出发沿B-C-A的路线向终点以每秒2个单位的速度运动,以EF为边向上(或向右)作等边三角形EFG.AH是△ABC中BC边上的高,两点运动时间为t秒,△EFG和△AHC有重合部分时,重合部分图形的周长为L.
如图,在菱形ABCD中,AB=6,∠ABC=60°,动点E、F同时从点B出发,其中点E从点B向点A以每秒1个单位的速度运动,点F从点B出发沿B-C-A的路线向终点以每秒2个单位的速度运动,以EF为边向上(或向右)作等边三角形EFG.AH是△ABC中BC边上的高,两点运动时间为t秒,△EFG和△AHC有重合部分时,重合部分图形的周长为L.