题目内容
14. 已知:如图,⊙O的半径OC垂直弦AB于点H,连接BC,过点A作弦AE∥BC,过点C作CD∥BA交EA延长线于点D,延长CO交AE于点F.
已知:如图,⊙O的半径OC垂直弦AB于点H,连接BC,过点A作弦AE∥BC,过点C作CD∥BA交EA延长线于点D,延长CO交AE于点F.(1)求证:CD为⊙O的切线;
(2)若BC=10,AB=16,求OF的长.
分析 (1)欲证明CD是⊙切线,只要证明CD⊥CO即可.
(2)连结B0.设OB=x,在RT△BHO中利用勾股定理求出x,再证明△CHB≌△FHA得CH=HF,CF=2CH,由此即可解决问题.
解答 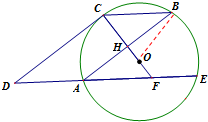 解:(1)∵OC⊥AB,AB∥CD,
解:(1)∵OC⊥AB,AB∥CD,
∴OC⊥DC,
∴CD是⊙O的切线.
(2)连结B0.
设OB=x,
∵AB=16,OC⊥AB,
∴HA=BH=8,
∵BC=10,
∴CH=6,
∴OH=x-6.
在RT△BHO中,∵OH2+BH2=OB2,
∴(x-6)2+82=x2
解得$x=\frac{25}{3}$
∵CB∥AE
∴∠CBH=∠FAH,
在△CHB和△FHA中,
$\left\{\begin{array}{l}{∠CBH=∠FAH}\\{∠CHB=∠AHF}\\{BH=AH}\end{array}\right.$,
∴△CHB≌△FHA
∴CH=HF,
∴CF=2CH=12
∴OF=CF-OC=12-$\frac{25}{3}=\frac{11}{3}$.
点评 本题考查切线的性质、全等三角形的判定和性质、垂径定理、勾股定理、平行线的性质等知识,解题的关键是记住切线的判定方法,利用勾股定理列出方程,把问题转化为方程解决,属于中考常考题型.

练习册系列答案
相关题目
6.书架上有2本小说,1本散文,从中随机抽取2本都是小说的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{2}{3}$ |
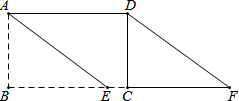 如图,矩形ABCD中,AD=5,AB=3,在BC边上取一点E,使BE=4,连结AE,沿AE剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
如图,矩形ABCD中,AD=5,AB=3,在BC边上取一点E,使BE=4,连结AE,沿AE剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD. 如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.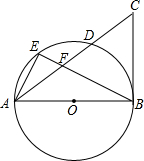 如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,E为$\widehat{AD}$上一点,连结AE、BE,BE交AC于点F,且∠AFE=∠EAB.
如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,E为$\widehat{AD}$上一点,连结AE、BE,BE交AC于点F,且∠AFE=∠EAB.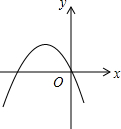 二次函数y=ax2+bx+c的图象如图,解不等式bx+a>0.
二次函数y=ax2+bx+c的图象如图,解不等式bx+a>0.