题目内容
2. 如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,∠A=30°,且AB、CE的长是方程x2+bx+c=0的两根,求b、c的值.
分析 (1)连接OD、DB,根据等腰三角形三线合一的性质得出AD=DC,根据三角形中位线定理得出OD∥BC,由此即可证明OD⊥DE.
(2)先求出AB、EC,再根据一元二次方程的根与系数关系即可解决问题.
解答 (1)证明: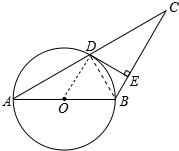 连接OD、DB.
连接OD、DB.
∵AB是直径,
∴∠ADB=90°,
∴BD⊥AC,
∵BA=BC,
∴AD=DC,
∵AO=OB
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∴DE是⊙O的切线.
(2)解:∵∠A=30°AB=BC=4,∠ADB=90°,
∴BD=2,∠ABD=∠ODB=60°,
∴∠EDB=30°,
∴BE=$\frac{1}{2}$BD=1,
∴EC=3,
∴AB+CE=4+3=7,AB•CE4×3=12,
∵AB、CE的长是方程x2+bx+c=0的两根,
∴b=-(AB+CE)=-7,c=AB•EC=12.
点评 本题考查切线的判定、等腰三角形的判定和性质、三角形中位线定理,直角三角形30度角性质、一元二次方程的根与系数关系定理等知识,解题的关键是添加辅助线,构造三角形中位线,属于中考常考题型.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
7.以下现象:①传送带上,瓶装饮料的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④在荡秋千的小朋友.其中属于平移的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
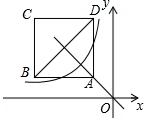 如图,正方形ABCD位于第二象限,边长为2,点A在直线y=-x上,点A的横坐标为-1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为-9≤k≤-1.
如图,正方形ABCD位于第二象限,边长为2,点A在直线y=-x上,点A的横坐标为-1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为-9≤k≤-1.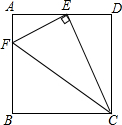 如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF=$\frac{1}{2}$.
如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF=$\frac{1}{2}$. 已知:如图,⊙O的半径OC垂直弦AB于点H,连接BC,过点A作弦AE∥BC,过点C作CD∥BA交EA延长线于点D,延长CO交AE于点F.
已知:如图,⊙O的半径OC垂直弦AB于点H,连接BC,过点A作弦AE∥BC,过点C作CD∥BA交EA延长线于点D,延长CO交AE于点F. 如图,AB是⊙O的直径,AB=2,CD与⊙O相切于点D,∠DAB=60°,点E在切线CD上,则当∠AEB最大时,AE=1.
如图,AB是⊙O的直径,AB=2,CD与⊙O相切于点D,∠DAB=60°,点E在切线CD上,则当∠AEB最大时,AE=1.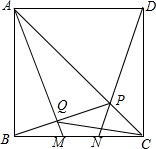 如图,M,N是正方形ABCD的边BC上两个动点,满足BM=CN,连结AC交DN于点P,连结AM交BP于点Q,若正方形的边长为1,则线段CQ的最小值是$\frac{\sqrt{5}-1}{2}$.
如图,M,N是正方形ABCD的边BC上两个动点,满足BM=CN,连结AC交DN于点P,连结AM交BP于点Q,若正方形的边长为1,则线段CQ的最小值是$\frac{\sqrt{5}-1}{2}$.