题目内容
9.已知关于x的方程x2+2(a-1)x+a2-9a-4=0的两根为x1、x2,且满足x1x2-3x1-3x2=0,求(1+$\frac{4}{{a}^{2}-4}$)•$\frac{a+2}{a}$的值.分析 先由韦达定理得到x1+x2=-2(a-1),x1x2=a2-9a-4代入x1x2-3x1-3x2=0中求出a,再化简(1+$\frac{4}{{a}^{2}-4}$)•$\frac{a+2}{a}$=$\frac{a}{a-2}$即可.
解答 解:根据韦达定理,得x1+x2=-2(a-1),x1x2=a2-9a-4,
∵x1x2-3x1-3x2x1x2-3(x1+x2)=0,
∴a2-9a-4-3×[-2(a-1)]=0,
∴a=5或a=-2(舍),
∴(1+$\frac{4}{{a}^{2}-4}$)•$\frac{a+2}{a}$
=(1+$\frac{4}{(a+2)(a-2)}$)×$\frac{a+2}{a}$
=$\frac{a+2}{a}$+$\frac{4}{a(a-2)}$
=$\frac{(a+2)(a-2)+4}{a(a-2)}$
=$\frac{{a}^{2}}{a(a-2)}$
=$\frac{a}{a-2}$
=$\frac{5}{5-2}$
=$\frac{5}{3}$.
点评 此题是根与系数的关系,主要考查了韦达定理,化简,解本题的关键是求出a的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.?ABCD的对角线相交于点O,下列结论错误的是( )
| A. | ?ABCD是中心对称图形 | B. | △AOB与△BOC的面积相等 | ||
| C. | △AOB≌△COD | D. | △AOB≌△BOC |
17.PM 2.5是指大气压中直径小于或等于0.0000025m的颗粒物,将它用科学记数法表示为( )
| A. | 0.25×10-7m | B. | 2.5×106m | C. | 2.5×10-6m | D. | 2.5×10-8m |
 如图,⊙P过平面直角坐标系原点O和x轴交于点A(8,0),和y轴交于点B(0,-6),⊙P的切线DC垂直于y轴,垂足为D,连接OC.
如图,⊙P过平面直角坐标系原点O和x轴交于点A(8,0),和y轴交于点B(0,-6),⊙P的切线DC垂直于y轴,垂足为D,连接OC.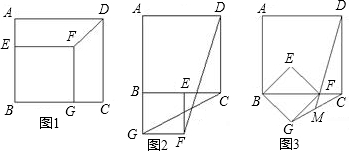
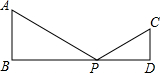 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?