题目内容
10.如果10b=n,那么称b为n的劳格数,记为b=d(n),由定义可知,10b=n 和b=d(n)所表示的b、n两个量之间具有同一关系,(1)根据定义,填空:d(10)=1,d(10-2)=-2
(2)劳格数具有如下性质:d(mn)=d(m)+d(n),d($\frac{m}{n}$)=d(m)-d(n)根据运算性质,填空
①$\frac{d({a}^{2})}{d(a)}$=2,(a为正数),②若d(2)=0.3010,d(4)=0.6020,d(5)=0.6990.
分析 (1)首先根据10b=10,求出b的值是多少,即可求出d(10)的值是多少;然后根据10b=10-2,求出b的值是多少,即可求出d(10-2)的值是多少.
(2)①根据d(mn)=d(m)+d(n),可得d(a2)=d(a)+d(a),据此求出算式的值是多少即可.
②首先根据d(2)=0.3010,d(4)=d(2)+d(2),求出d(4)的值是多少;然后根据d(2×1)=d(2)+d(1),求出d(1)的值是0;最后根据d(5))=d($\frac{20}{4}$)=d(20)-d(4)=d(10)+d(2)-d(4),求出d(5)的值是多少即可.
解答 解:(1)∵10b=10,
∴b=1,
∴d(10)=1.
∵10b=10-2,
∴b=-2,
∴d(10-2)=-2.
(2)①$\frac{d({a}^{2})}{d(a)}$
=$\frac{d(a)+d(a)}{d(a)}$
=$\frac{2d(a)}{d(a)}$
=2
②∵d(2)=0.3010,
∴d(4)=d(2)+d(2)
=0.3010+0.3010
=0.6020
∵d(2×1)=d(2)+d(1),
∴d(2)=d(2)+d(1),
∴d(1)=0,
∴d(5)=d($\frac{20}{4}$)
=d(20)-d(4)
=d(10)+d(2)-d(4)
=1+0.3010-0.6020
=1.3010-0.6020
=0.6990
故答案为:1、-2;2、0.6020、0.6990.
点评 (1)此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
(2)解答此题的关键还要明确劳格数的含义和应用,要熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.在?ABCD中,如果添加一个条件,就可推出?ABCD是矩形,那么添加的条件可以是( )
| A. | AB=BC | B. | AC=BD | C. | AC⊥BD | D. | AB⊥BD |
12.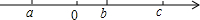 实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
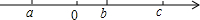 实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )| A. | -a<b<c | B. | ab<ac | C. | -a+b>-a+c | D. | |a-b|<|a-c| |
 如图,已知A(1,0)、C(0,1)、B(m,0)且m>1,在平面内求一点P,使得以A、B、C、P为顶点的四边形是平行四边形,则点P的坐标为(m-1,1)或(1-m,1)或(m+1,-1).
如图,已知A(1,0)、C(0,1)、B(m,0)且m>1,在平面内求一点P,使得以A、B、C、P为顶点的四边形是平行四边形,则点P的坐标为(m-1,1)或(1-m,1)或(m+1,-1). 如图,在?ABCD中,EF经过对角线的交点O,且EF⊥AC分别交CD、AB于点E,F,试说明四边形AECF是菱形.
如图,在?ABCD中,EF经过对角线的交点O,且EF⊥AC分别交CD、AB于点E,F,试说明四边形AECF是菱形.