题目内容
4.先化简再求值:$\frac{a}{a+2}-\frac{{a}^{2}-1}{{a}^{2}+2a}÷\frac{a-1}{a}$,其中a=$\sqrt{5}$-2.分析 先将分式分子、分母因式分解、同时将除法转化为乘法,约分后计算同分母分式相减即可化简,最后将a的值代入后分母有理化即可.
解答 解:原式=$\frac{a}{a+2}$-$\frac{(a+1)(a-1)}{a(a+2)}$×$\frac{a}{a-1}$
=$\frac{a}{a+2}$-$\frac{a+1}{a+2}$
=$\frac{a-a-1}{a+2}$
=-$\frac{1}{a+2}$,
当a=$\sqrt{5}$-2时,
原式=-$\frac{1}{\sqrt{5}-2}$
=-$\frac{\sqrt{5}+2}{(\sqrt{5}-2)(\sqrt{5}+2)}$
=-$\sqrt{5}$-2.
点评 本题主要考查分式的化简求值能力,熟练掌握分式混合运算的步骤是解题的根本.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.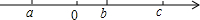 实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
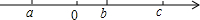 实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )| A. | -a<b<c | B. | ab<ac | C. | -a+b>-a+c | D. | |a-b|<|a-c| |
3.下列关于x的方程以定是一元一次方程的是( )
| A. | $\frac{2}{x}$-x=1 | B. | (a2+1)x+b=0 | C. | ax2=b | D. | $\sqrt{2x+1}=5$ |