题目内容
7.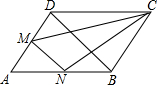 如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )
如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )| A. | S△DMC>S△BNC | B. | S△DMC=S△BNC | C. | S△DMC<S△BNC | D. | 无法确定 |
分析 利用平行四边形的性质以及平行线分线段成比例定理得出MD=kAD,NB=kAB,进而分别表示出S△MDC,S△NBC,即可得出答案.
解答 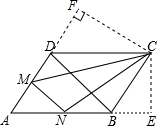 解:过点C作CF⊥AD于点F,过点C作CE⊥AB于点E,
解:过点C作CF⊥AD于点F,过点C作CE⊥AB于点E,
∵MN∥BD,
∴设$\frac{MD}{AD}$=$\frac{NB}{AB}$=k,则MD=kAD,NB=kAB,
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD=BC,AB=DC,
∴∠FDC=∠CBE,
∴FC=DC•sin∠FDC,EC=BC•sin∠CBE,
∴S△MDC=$\frac{1}{2}$MD•DC•sin∠FDC=$\frac{1}{2}$•kAD•DC•sin∠FDC,
S△NBC=$\frac{1}{2}$NB•BC•sin∠CBE=$\frac{1}{2}$•kAB•BC•sin∠CBE,
∴S△MDC=S△NBC.
故选B.
点评 此题主要考查了平行四边形的性质以及三角形面积表示方法,正确表示出S△MDC,S△NBC是解题关键.

练习册系列答案
相关题目
16.下列四个实数中,最小的数是( )
| A. | -2 | B. | -$\sqrt{5}$ | C. | -1 | D. | 0 |
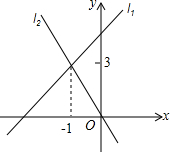 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式0<k2x<k1x+b的解集为-1<x<0.
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式0<k2x<k1x+b的解集为-1<x<0. 如图,正方形ABCD的边长为2,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为2-$\sqrt{2}$.
如图,正方形ABCD的边长为2,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为2-$\sqrt{2}$.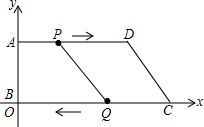 如图,在平面直角坐标系中,O为原点,已知A(0,8),D(24,8),C(26,0),动点P从点A开始沿AD边向点D以1cm/秒的速度运动;动点Q从点C开始沿CO边向点O以3cm/秒的速度运动,若P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.
如图,在平面直角坐标系中,O为原点,已知A(0,8),D(24,8),C(26,0),动点P从点A开始沿AD边向点D以1cm/秒的速度运动;动点Q从点C开始沿CO边向点O以3cm/秒的速度运动,若P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.