题目内容
2.已知OA⊥OB,∠AOC:∠AOB=2:3,则∠BOC的度数为30°或150°.分析 根据垂直关系可得∠AOB=90°,再由∠AOC:∠AOB=2:3,可得∠AOC=120°,然后再分两种情况进行计算即可.
解答 解:如图,∠AOC的位置有两种:一种是∠AOC在∠AOB内,一种是在∠AOB外.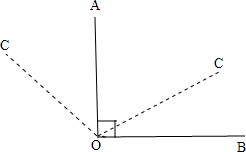
∵OA⊥OB,
∴∠AOB=90°,
①当∠AOC在∠AOB内,
∵∠AOC:∠AOB=2:3,
∴∠AOC=$\frac{2}{3}∠AOB$=60°,
∴∠BOC=90°-∠AOC=30°;
②当∠AOC在∠AOB外,
∵∠AOC:∠AOB=2:3,
∴∠AOC=$\frac{2}{3}∠AOB$=60°,
∴∠BOC=90°+∠AOC=150°.
故答案为:30°或150°.
点评 此题主要考查了垂线的定义:当两条直线相交所成的四个角中,有一个角是直角时,即两条直线互相垂直.同时做这类题时一定要结合图形.

练习册系列答案
相关题目
7.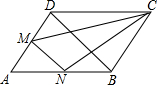 如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )
如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )
 如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )
如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )| A. | S△DMC>S△BNC | B. | S△DMC=S△BNC | C. | S△DMC<S△BNC | D. | 无法确定 |
14.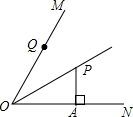 如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )
如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )
 如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )
如图,∠MON=60°,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若OP=4,则PQ的最小值为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | 2 | D. | $\sqrt{3}$ |

 已知O为三边垂直平分线交点,∠BAC=80°,则∠BOC=160°.
已知O为三边垂直平分线交点,∠BAC=80°,则∠BOC=160°.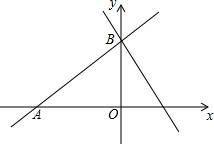 已知一次函数的图象与x轴、y轴分别交于点A(-2,0)、B(0,3).
已知一次函数的图象与x轴、y轴分别交于点A(-2,0)、B(0,3). 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为16cm2,则△BEF的面积:4cm2.
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为16cm2,则△BEF的面积:4cm2.