题目内容
17.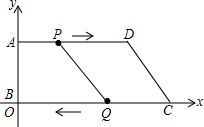 如图,在平面直角坐标系中,O为原点,已知A(0,8),D(24,8),C(26,0),动点P从点A开始沿AD边向点D以1cm/秒的速度运动;动点Q从点C开始沿CO边向点O以3cm/秒的速度运动,若P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.
如图,在平面直角坐标系中,O为原点,已知A(0,8),D(24,8),C(26,0),动点P从点A开始沿AD边向点D以1cm/秒的速度运动;动点Q从点C开始沿CO边向点O以3cm/秒的速度运动,若P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.(1)求经过多次时间时,四边形PQCD为平行四边形;
(2)当四边形PQCD为平行四边形时,求PQ所在直线的函数解析式.
分析 (1)根据一组对边平行且相等的四边形是平行四边形列出算式,解出t得到答案;
(2)确定点P、Q的坐标,运用待定系数法求解即可.
解答 解:(1)设t秒后四边形PQCD为平行四边形,
∵当PD=QC时,四边形PQCD为平行四边形,
∴24-t=3t,
解得,t=6;
(2)6秒后,点P的坐标为:(6,8),
点Q的坐标为:(8,0),
设直线PQ的解析式为:y=kx+b,
$\left\{\begin{array}{l}{6k+b=8}\\{8k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-4}\\{b=32}\end{array}\right.$,
∴直线PQ的解析式为:y=-4x+32.
点评 本题考查的是一次函数的综合应用,灵活运用待定系数法求一次函数解析式是解题的关键,注意平行四边形的判定定理的正确运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.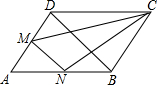 如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )
如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )
 如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )
如图,BD为?ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC与S△BNC的大小关系是( )| A. | S△DMC>S△BNC | B. | S△DMC=S△BNC | C. | S△DMC<S△BNC | D. | 无法确定 |
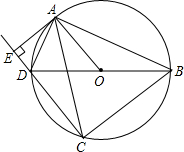 如图所示,四边形ABCD是⊙O的内接四边形,AB=AC,BD是⊙O的直径,延长CD,过点A作AE⊥CD于点E.
如图所示,四边形ABCD是⊙O的内接四边形,AB=AC,BD是⊙O的直径,延长CD,过点A作AE⊥CD于点E.
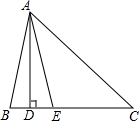 如图,△ABC中,AD⊥BC,AE平分∠BAC.
如图,△ABC中,AD⊥BC,AE平分∠BAC.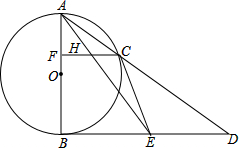 如图,已知C是以AB为直径的圆O上一点,CF⊥AB于点F,直线AC与过点B的切线相交于点D,E为BD的中点,连接AE交CF于点H,连接CE.
如图,已知C是以AB为直径的圆O上一点,CF⊥AB于点F,直线AC与过点B的切线相交于点D,E为BD的中点,连接AE交CF于点H,连接CE.