题目内容
分解因式:
(1)a2(x-y)+b2(y-x)
(2)x2-xy+
y2-1.
(1)a2(x-y)+b2(y-x)
(2)x2-xy+
| 1 |
| 4 |
考点:提公因式法与公式法的综合运用,因式分解-分组分解法
专题:
分析:(1)首先提取公因式x-y,再利用平方差公式进行分解即可;
(2)首先把前三项利用完全平方进行分解,再利用平方差进行二次分解即可.
(2)首先把前三项利用完全平方进行分解,再利用平方差进行二次分解即可.
解答:解:(1)原式=a2(x-y)-b2(x-y)
=(x-y)(a2-b2)
=(x-y)(a+b)(a-b);
(2)原式=(x-
y)2-1
=(x-
y+1)(x-
y-1).
=(x-y)(a2-b2)
=(x-y)(a+b)(a-b);
(2)原式=(x-
| 1 |
| 2 |
=(x-
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了用提公因式法、分组分解法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
相关题目
 如图,已知AB∥CD,∠B=∠D=120°,求∠BOD的度数.
如图,已知AB∥CD,∠B=∠D=120°,求∠BOD的度数.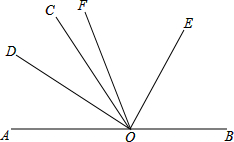 如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.求:
如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.求: