题目内容
七年级(1)班的全体同学集体步行去市博物馆参加科技活动.小刚担任通讯员.在队伍中,他先数了一下他前后的人数,发现前面人数是后面的两倍,他往前超了8名同学后,发现前面的人数和后面的人数一样.
(1)七年级(1)班共有多少名同学?
(2)这列学生要过一座长60米的大桥,前进速度为2米/秒,从第一名同学刚上桥到全体通过大桥用了96秒时间,学生队伍的全长为多少米?
(3)在(2)的条件下,排在队尾的小明想把一则通知送到队伍最前面的小丽同学,若小明从队尾追赶小丽的速度是5米/秒,他能在1分钟内追上小丽吗?说明你的理由.
(1)七年级(1)班共有多少名同学?
(2)这列学生要过一座长60米的大桥,前进速度为2米/秒,从第一名同学刚上桥到全体通过大桥用了96秒时间,学生队伍的全长为多少米?
(3)在(2)的条件下,排在队尾的小明想把一则通知送到队伍最前面的小丽同学,若小明从队尾追赶小丽的速度是5米/秒,他能在1分钟内追上小丽吗?说明你的理由.
考点:一元一次方程的应用
专题:应用题
分析:(1)设七年级(1)班队伍中小刚后面人数有x名,前面有2x名,根据题意列出方程,求出方程的解即可得到结果;
(2)设队伍全长为y米,根据题意列出关于y的方程,求出方程的解即可得到结果;
(3)设小明z秒追上小丽,根据题意列出关于z的方程,求出方程的解即可做出判断.
(2)设队伍全长为y米,根据题意列出关于y的方程,求出方程的解即可得到结果;
(3)设小明z秒追上小丽,根据题意列出关于z的方程,求出方程的解即可做出判断.
解答:解:(1)设七年级(1)班队伍中小刚后面人数有x名,前面有2x名,
根据题意得:根据题意得:x+8=2x-8,
解得:x=16,
则七年级(1)班共有16+32+1=49(人);
(2)设队伍全长为y米,
根据题意得:60+y=2×96,
解得:y=132,
则队伍全长为132米;
(3)设小明z秒追上小丽,
根据题意得:(5-2)z=132,
解得:z=44,
则他能在1分钟内追上小丽.
根据题意得:根据题意得:x+8=2x-8,
解得:x=16,
则七年级(1)班共有16+32+1=49(人);
(2)设队伍全长为y米,
根据题意得:60+y=2×96,
解得:y=132,
则队伍全长为132米;
(3)设小明z秒追上小丽,
根据题意得:(5-2)z=132,
解得:z=44,
则他能在1分钟内追上小丽.
点评:此题考查了一元一次方程的应用,找出每一个等量关系是解本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知x=1是二次方程(m2-1)x2-mx+m2=0的一个根,那么m的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、
|
 如图,△AOB是由△A1O1B1平移后得到的,已知点A1的坐标为(-3,-1).
如图,△AOB是由△A1O1B1平移后得到的,已知点A1的坐标为(-3,-1). 抛物线y=-x2+bx+c的图象如图,若将其向左平移2个单位,再向下平移3个单位,则平移后的解析式为
抛物线y=-x2+bx+c的图象如图,若将其向左平移2个单位,再向下平移3个单位,则平移后的解析式为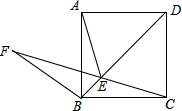 如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论:
如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论: 如图,在△ABC中,AB=AC,CD⊥AB于点D,CE为△ACD的角平分线,EF⊥BC于点F,EF交CD于点G.求证:BE=CG.
如图,在△ABC中,AB=AC,CD⊥AB于点D,CE为△ACD的角平分线,EF⊥BC于点F,EF交CD于点G.求证:BE=CG.