题目内容
15．2014年长江外滩有块面积为100公顷的湿地，为了保护生态系统，从2015年开始，市政府通过退耕还林来扩大这片湿地的面积．计划到2016年湿地面积达到225公顷．（1）求2015、2016两年这片湿地面积的年平均增长率；
（2）如果按照这样的速度增加湿地面积，到2017年这片湿地的面积将达到多少公顷？
分析 （1）根据湿地面积=提高前的湿地面积（1+增长率），设年平均增长率为x，则2015年的湿地面积是100（1+x），2016年的湿地面积是100（1+x）2，即可列方程求得增长率；
（2）利用求得的百分率，得出2017年的湿地面积是225（1+x）．
解答 解：（1）设2015、2016两年这片湿地面积的年平均增长率为x，根据题意可得：
100（1+x）2=225，
解得：x1=0.5，x2=-2.5（不合题意舍去）．
答：2015、2016两年这片湿地面积的年平均增长率为：50%；
（2）由（1）得：225×（1+0.5）=337.5（公顷）．
答：2017年这片湿地的面积将达到337.5公顷．
点评 此题考查了一元二次方程的应用，运用增长率（下降率）的模型解题．读懂题意，找到等量关系准确的列出方程是解题的关键．
练习册系列答案
相关题目
5．
如图，已知∠A=n°，若P1点是∠ABC和外角∠ACE的角平分线的交点，P2点是∠P1BC和外角∠P1CE的角平分线的交点，P3点是∠P2BC和外角∠P2CE的交点…依此类推，则∠Pn=（ ）
如图，已知∠A=n°，若P1点是∠ABC和外角∠ACE的角平分线的交点，P2点是∠P1BC和外角∠P1CE的角平分线的交点，P3点是∠P2BC和外角∠P2CE的交点…依此类推，则∠Pn=（ ）| A． | $\frac{n°}{2n}$ | B． | $\frac{n°}{2^n}$ | C． | $\frac{n°}{{{2^{n-1}}}}$ | D． | $\frac{n°}{2（n-1）}$ |
如图，直线l外一点A及直线上一点B，试用尺规作图法，在直线l上求作一点P，使得△PAB是等腰三角形，则符合条件的点P有多少个？在图中作出点P的位置，并写出所有的等腰三角形．（注：点P的位置分别用P1，P2，P3…来表示）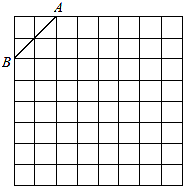
如图是规格为8×8的正方形网格，请在所给网格中按下列要求操作：