题目内容
7．计算：（1）$\root{3}{-8}+{（\frac{1}{4}）^{-1}}-\sqrt{25}$
（2）$\sqrt{（-4）^{2}}$-（-1）2-（$\sqrt{3}$-1）0+$\root{3}{-27}$．
分析 （1）结合立方根以及负整数指数幂的性质和二次根式的性质化简求出答案；
（2）利用二次根式的性质以及立方根的性质和零指数幂的性质化简求出答案．
解答 解：（1）$\root{3}{-8}+{（\frac{1}{4}）^{-1}}-\sqrt{25}$
=-2+4-5
=-3；
（2）原式=4-1-1+（-3）
=-1．
点评 此题主要考查了实数运算，正确化简各数是解题关键．
练习册系列答案
相关题目
2．
如图，在扇形OAB中，半径OA=4，∠AOB=120°，点C在$\widehat{AB}$上，OD⊥AC于点D，OE⊥BC于点E，当点C从点A运动到点B时，线段DE长度的变化情况是（ ）
如图，在扇形OAB中，半径OA=4，∠AOB=120°，点C在$\widehat{AB}$上，OD⊥AC于点D，OE⊥BC于点E，当点C从点A运动到点B时，线段DE长度的变化情况是（ ）| A． | 先变小，后变大 | B． | 先变大，后变小 | ||
| C． | DE与OD的长度保持相等 | D． | 固定不变 |
12．观察下表：
我们把某格中字母的和所得到的多项式称为特征多项式，例如第1格的“特征多项式”为4x+y．回答下列问题：
（1）第2格的“特征多项式”为9x+4y，第n格的“特征多项式”为（n+1）2x+n2y；（n为正整数）
（2）若第1格的“特征多项式”的值为-8，第2格的“特征多项式”的值为-11．
①求x，y的值；
②在此条件下，第n格的特征多项式是否有最小值？若有，求最小值和相应的n值；若没有，请说明理由．
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x | x x x y y x x y y x x x | x x x x y y y x x y y y x x y y y x x x x | … |
（1）第2格的“特征多项式”为9x+4y，第n格的“特征多项式”为（n+1）2x+n2y；（n为正整数）
（2）若第1格的“特征多项式”的值为-8，第2格的“特征多项式”的值为-11．
①求x，y的值；
②在此条件下，第n格的特征多项式是否有最小值？若有，求最小值和相应的n值；若没有，请说明理由．
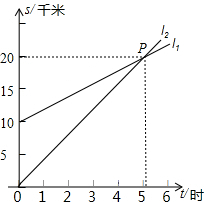如图，l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系，根据图象填空：