题目内容
4．$\frac{16}{9}$的平方根是±$\frac{4}{3}$，$\sqrt{64}$的立方根是2，4.24970≈4.25（精确到百分位）分析 前两式利用平方根、立方根的定义计算得到结果，最后一式根据近似数位确定出近似数即可．
解答 解：$\frac{16}{9}$的平方根是±$\frac{4}{3}$，$\sqrt{64}$=8，8的立方根是2；4.24970≈4.25，
故答案为：±$\frac{4}{3}$；2；4.25．
点评 此题考查了立方根，近似数和有效数字，平方根，以及算术平方根，熟练掌握各自的定义是解本题的关键．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
如图，△ABC中，∠C=90°．
12．观察下表：
我们把某格中字母的和所得到的多项式称为特征多项式，例如第1格的“特征多项式”为4x+y．回答下列问题：
（1）第2格的“特征多项式”为9x+4y，第n格的“特征多项式”为（n+1）2x+n2y；（n为正整数）
（2）若第1格的“特征多项式”的值为-8，第2格的“特征多项式”的值为-11．
①求x，y的值；
②在此条件下，第n格的特征多项式是否有最小值？若有，求最小值和相应的n值；若没有，请说明理由．
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x | x x x y y x x y y x x x | x x x x y y y x x y y y x x y y y x x x x | … |
（1）第2格的“特征多项式”为9x+4y，第n格的“特征多项式”为（n+1）2x+n2y；（n为正整数）
（2）若第1格的“特征多项式”的值为-8，第2格的“特征多项式”的值为-11．
①求x，y的值；
②在此条件下，第n格的特征多项式是否有最小值？若有，求最小值和相应的n值；若没有，请说明理由．
如图是一个外轮廓为长方形的机器零件的平面示意图，根据图中的尺寸（单位：cm），计算两个圆孔中的A和B的距离为10cm．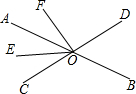
如图，AB、CD相交于点O，OE是∠AOC的平分线，∠BOD=70°，∠EOF=65°．求∠AOF的度数．
