题目内容
19. 平面直角坐标系中,点A在函数y1=$\frac{2}{x}$(x>0)的图象上,点B在y2=-$\frac{2}{x}$(x<0)的图象上,设A的横坐标为a,B的横坐标为b.
平面直角坐标系中,点A在函数y1=$\frac{2}{x}$(x>0)的图象上,点B在y2=-$\frac{2}{x}$(x<0)的图象上,设A的横坐标为a,B的横坐标为b.(1)当|a|=|b|=5时,求△OAB的面积;
(2)当AB∥x轴时,求△OAB的面积.
分析 (1)如图1,作AC⊥x轴于C,BD⊥x轴于D,先旅游反比例函数解析式确定当A(5,$\frac{2}{5}$),B(-$\frac{2}{5}$,5),再利用反比例函数系数k的几何意义得到S△BOD=S△AOC=1,然后利用S△AOB=S梯形ABDC-S△BOD-S△AOC进行计算;
(2)如图2,AB交y轴于H,根据反比例函数系数k的几何意义,利用S△AOB=S△BOH+S△AOH进行计算即可.
解答 解:(1)如图1,作AC⊥x轴于C,BD⊥x轴于D,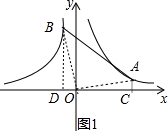
∵|a|=|b|=5,
∴a=5,b=5,
当x=5时,y1=$\frac{2}{x}$=$\frac{2}{5}$,则A(5,$\frac{2}{5}$),
当y=5时,-$\frac{2}{x}$=5,解得x=-$\frac{2}{5}$,则B(-$\frac{2}{5}$,5),
∵S△BOD=$\frac{1}{2}$×2=1,S△AOC=$\frac{1}{2}$×2=1,
∴S△AOB=S梯形ABDC-S△BOD-S△AOC=$\frac{1}{2}$×($\frac{2}{5}$+5)(5+$\frac{2}{5}$)-1-1=$\frac{629}{50}$;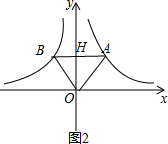
(2)如图2,AB交y轴于H,
∵AB∥x轴,
∴S△AOB=S△BOH+S△AOH=$\frac{1}{2}$×2+$\frac{1}{2}$×2=2.
点评 本题考查了反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第一周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元,不少于5340元的金额再采购这两种型号的电风扇共30台,求A、B两种型号的电风扇的采购方案;
(3)在(2)的条件下,超市销售完这30台电风扇,用所获利润再次购进A/B两种型号的电风扇且恰好全部售出,请直接写出再次销售的A、B两种型号的电风扇各多少台所获最大利润?最大利润是多少?

 如图所示,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(6,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=$\frac{1}{3}$.
如图所示,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(6,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=$\frac{1}{3}$.