题目内容
4.如图1,线段AB被P1,P2,P3,…,Pn-1分成n(n≥2)份,设AP1=x,若P1P2=x+1,P2P3=x=2,P3P4=x+3,…,Pn-1B=x+(n-1),则称线段AB为n阶线段;其中AP1的长x叫做起分量,n称为线段AB的阶数.如:线段AB=9,可被P1,P2分为长为2,3,4三条线段(如图2),即:9=2+3+4,则AB称为起分量为2的3阶线段;也可被P1分为长4,5两条线段(如图3),即:9=4+5,则AB也可称为起分量为4的2阶线段.
(1)求起分量为7的3阶线段长;
(2)求长为39的6阶线段的起分量;
(3)长为15的线段可以是几阶线段,起分量分别是多少?(简要说明理由)
(4)直接写出长为2016,起分量为1的线段的阶数.
分析 (1)求三个连续整数的和,最小的数为7;
(2)6个连续的整数的和为39,设最小的数为x,列方程可求得;
(3)分三种情况:连续整数和为15,列式计算;
(4)设阶数为a,则从1加到a的和为2016,列式得一元二次方程,解出即可.
解答 解:(1)7+8+9=24,
∴起分量为7的3阶线段长为24;
(2)设起分量为x,
则x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)=39,
x=4,
∴长为39的6阶线段的起分量为4;
(3)①15=1+2+3+4+5,
∴长为15的线段可以是5阶线段,起分量分别是1,
②15=4+5+6,
∴长为15的线段可以是3阶线段,起分量分别是4,
③15=7+8,
∴长为15的线段可以是2阶线段,起分量分别是7,
(4)设长为2016,起分量为1的线段的阶数为a,
则1+2+3+…+a=2016,
$\frac{a(a+1)}{2}$=2016,
a2+a-4032=0,
(a+64)(a-63)=0,
a1=-64(舍) a2=63,
∴长为2016,起分量为1的线段的阶数为63.
点评 本题是图形的变化类规律题,虽然题意叙述比较多,但难度不大;此类题要认真观察、仔细思考,善用联想来解决这类问题;发现与连续整数的和有关,找出规律,依次解答.

练习册系列答案
相关题目
12.某海滨浴场有100个遮阳伞,每个每天收租费10元时,可全部租出;若每个每天提高2元,则减少10个伞租出;若每个每天收费再提高2元,则再减少10个伞租出…为了投资最少而获利最大,每个每天应提高6.
16.某棉纺厂为了解一批锦花的质量,从中随机抽取了20根锦花纤维进行侧量,其长度x(单位;mm)的数据分布如表.完成表格.并求这些锦花纤维的平均长度.
| 棉花纤维长度x | 组中值 | 频数 |
| 0≤x<8 | 4 | 2 |
| 8≤x<16 | 12 | 2 |
| 16≤x<24 | 20 | 2 |
| 24≤x<32 | 28 | 12 |
| 32≤x<40 | 36 | 2 |
14.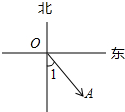 如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )
如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )
 如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )
如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )| A. | 商船在海岛的北偏西50°方向 | B. | 海岛在商船的北偏西40°方向 | ||
| C. | 海岛在商船的东偏南50°方向 | D. | 商船在海岛的东偏南40°方向 |

 平面直角坐标系中,点A在函数y1=$\frac{2}{x}$(x>0)的图象上,点B在y2=-$\frac{2}{x}$(x<0)的图象上,设A的横坐标为a,B的横坐标为b.
平面直角坐标系中,点A在函数y1=$\frac{2}{x}$(x>0)的图象上,点B在y2=-$\frac{2}{x}$(x<0)的图象上,设A的横坐标为a,B的横坐标为b. 如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=4,BG=3,点F是AE的中点,连接DF,求线段DF的长.
如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=4,BG=3,点F是AE的中点,连接DF,求线段DF的长.