题目内容
3. 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为8.
分析 (1)根据图形平移的性质画出△A′B′C′即可;
(2)找出线段AB的中点D,连接CD即可;
(3)过点A向线段BC所在的直线作垂线,垂足为点E;
(4)利用矩形的面积减去两个顶点上三角形的面积即可.
解答 解: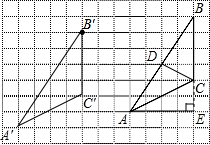 (1)如图所示,△A′B′C′即为所求;
(1)如图所示,△A′B′C′即为所求;
(2)如图,线段CD即为AB边上的中线;
(3)如图,线段AE即为BC边上的高;
(4)S△A′B′C′=4×6-$\frac{1}{2}$×2×4-$\frac{1}{2}$×4×6=24-4-12=8.
故答案为:8.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
14.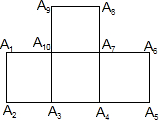 如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.
如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.
 如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.
如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.| A. | 18 | B. | 22 | C. | 24 | D. | 26 |
18. 如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
 如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )| A. | $\frac{AD}{BC}=\frac{CE}{DF}$ | B. | $\frac{AD}{BE}=\frac{BC}{AF}$ | C. | $\frac{AB}{CD}=\frac{CD}{EF}$ | D. | $\frac{AD}{BC}=\frac{DF}{CE}$ |
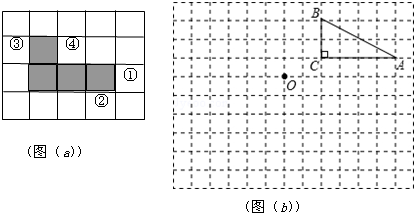
 如图,已知AO⊥BC,DO⊥OE,若∠1=56°,则∠2=56°.
如图,已知AO⊥BC,DO⊥OE,若∠1=56°,则∠2=56°.