题目内容
18．
如图，AB为⊙O的直径，△ABC内接于⊙O，点D为弧CAB上一点，若∠ABC=55°，则∠CDB=35度．
分析 根据圆周角定理求出∠ACB=90°，根据直角三角形的性质求出∠A的度数，根据同弧所对的圆周角相等得到答案．
解答 解：∵AB为⊙O的直径，
∴∠ACB=90°，又∠ABC=55°，
∴∠A=35°，
∴∠CDB=35°，
故答案为：35．
点评 本题考查的是圆周角定理，掌握直径所对的圆周角是直角、同弧所对的圆周角相等是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
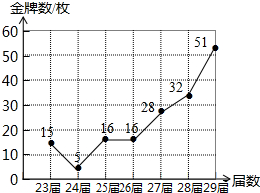从1984年起，我国先后参加了第23届夏季奥运会，取得了骄人的成绩．如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图，观察统计图可得：与上一届相比增长量最大的是第29届夏季奥运会，比它的上一届增加了19枚金牌．
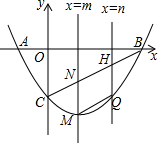如图，在平面直角坐标系中，抛物线y=x2-2x-3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，直线x=m（m＞0），直线x=n（n＞0）（m＜n）分别交线段BC于N点、H点，交抛物线于M点、Q点．当NH∥MQ时，求m+n的值．
如图，将三角形纸板ABC沿直线AB向右平行移动，使∠A到达∠B的位置，若∠CAB=50°，∠ABC=100°，则∠CBE的度数为30．
7．二次函数y=-3x2-6x+5的图象的顶点坐标是（ ）
| A． | （-1，2） | B． | （1，-4） | C． | （-1，8） | D． | （1，8） |
8．如果$\frac{a}{b}$=$\frac{c}{d}$，那么下列各式中不成立的是（ ）
| A． | $\frac{{a}^{2}}{{b}^{2}}$=$\frac{{c}^{2}}{{d}^{2}}$ | B． | $\frac{a}{b}$=$\frac{c+1}{d+1}$ | C． | $\frac{a+b}{b}$=$\frac{c+d}{d}$ | D． | $\frac{am}{b}$=$\frac{cm}{d}$ |