题目内容
19.在一个不透明的盒子里,装有四个分别标有数字-2,-1,1,4的小球,它们的形状、大小、质地等完全相同,小强先从盒子里随机取出一个小球,记下数字为a;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为b.(1)用列表法或画树状图表示出(a,b)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(a,b)落在二次函数y=x2的图象上的概率;
(3)求小强、小华各取一次小球所确定的数a,b满足直线y=ax+b经过一、二、三象限的概率.
分析 (1)利用树状图展示所有16种等可能的结果;
(2)根据二次函数图象上点的坐标特征得到点(-2,4),(-1,1),(1,1)落在二次函数y=x2的图象上,然后根据概率公式求解;
(3)根据一次函数图象与系数的关系可得到a>0,b>0,则点(1,1),(1,4),(4,1),(4,4)满足直线y=ax+b经过一、二、三象限,然后根据概率公式求解.
解答 解:(1)画树状图如下: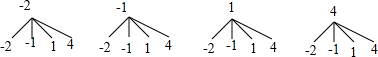
共有16种等可能的结果,它们为(-2,-2)、(-2,-1)、(-2,1)、(-2,4)、(-1,-2)、(-1,-1)、(-1,1)、(-1,4)、(1,-2)、(1,-1)、(1,1)、(1,4)、(4,-2)、(4,-1)、(4,1)、(4,4);
(2)落在二次函数y=x2的图象上的点有(-2,4),(-1,1),(1,1),
所以落在二次函数y=x2的图象上的概率=$\frac{3}{16}$;
(3)满足直线y=ax+b经过一、二、三象限的点有(1,1),(1,4),(4,1),(4,4),
所以满足直线y=ax+b经过一、二、三象限的概率=$\frac{4}{16}$=$\frac{1}{4}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了一次函数图象与系数的关系和二次函数图象上点的坐标特征.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
9.下面图形中,三棱柱的平面展开图为( )
| A. |  | B. |  | C. |  | D. |  |
7.若等边三角形ABC内接于⊙O,点P在$\widehat{CAB}$上(P不与B、C重合),则∠BPC等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
14.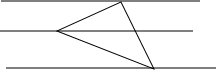 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )| A. | 3 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
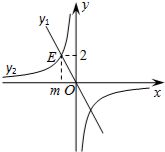 如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2).
如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2). 如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.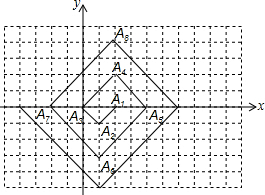 如图,在一单位长度为1的方格纸上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜边在x轴上,斜边长分别为2,4,6…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0).则依图中所示规律,A2016的坐标是(2,1008).
如图,在一单位长度为1的方格纸上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜边在x轴上,斜边长分别为2,4,6…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0).则依图中所示规律,A2016的坐标是(2,1008).