题目内容
14.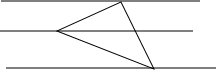 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )| A. | 3 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 作BD⊥a于D,CE⊥a于E则∠BDA=∠AEC=90°,证出∠ABD=∠CAE,由AAS证明△ABD≌△CAE,得出对应边相等AE=BD=1,由勾股定理求出AC,再由勾股定理求出BC即可.
解答 解:如图所示:作BD⊥a于D,CE⊥a于E,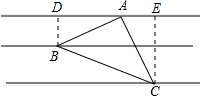
则∠BDA=∠AEC=90°,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠CAE+∠BAD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,$\left\{\begin{array}{l}{∠BDA=∠AEC}{\;}\\{∠ABD=∠CAE}{\;}\\{AB=AC}{\;}\end{array}\right.$,
∴△ABD≌△CAE(AAS),
∴AE=BD=1,
∵CE=2,
∴由勾股定理得:AB=AC=,$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{10}$.
故选:B.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质、勾股定理;熟练掌握勾股定理,通过作辅助线证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
5. 如图,在平面直角坐标系xOy中,点A的坐标为(-1,2),AB⊥x轴于点B.以原点O为位似中心,将△OAB放大为原来的2倍,得到△OA1B1,且点A1在第二象限,则点A1的坐标为( )
如图,在平面直角坐标系xOy中,点A的坐标为(-1,2),AB⊥x轴于点B.以原点O为位似中心,将△OAB放大为原来的2倍,得到△OA1B1,且点A1在第二象限,则点A1的坐标为( )
 如图,在平面直角坐标系xOy中,点A的坐标为(-1,2),AB⊥x轴于点B.以原点O为位似中心,将△OAB放大为原来的2倍,得到△OA1B1,且点A1在第二象限,则点A1的坐标为( )
如图,在平面直角坐标系xOy中,点A的坐标为(-1,2),AB⊥x轴于点B.以原点O为位似中心,将△OAB放大为原来的2倍,得到△OA1B1,且点A1在第二象限,则点A1的坐标为( )| A. | (-2,4) | B. | ($-\frac{1}{2}$,1) | C. | (2,-4) | D. | (2,4) |
 高铁的开通,给滕州市民带来了极大的方便,“元旦”期间,乐乐和明明相约到济南的某游乐园游玩,乐乐乘私家车从滕州出发1小时后,明明乘坐高铁从滕州出发,先到济南火车西站,然后再乘出租车到游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开滕州的距离y(千米)与乘车时间t(小时)的关系如图所示,请结合图象解决下面问题:
高铁的开通,给滕州市民带来了极大的方便,“元旦”期间,乐乐和明明相约到济南的某游乐园游玩,乐乐乘私家车从滕州出发1小时后,明明乘坐高铁从滕州出发,先到济南火车西站,然后再乘出租车到游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开滕州的距离y(千米)与乘车时间t(小时)的关系如图所示,请结合图象解决下面问题: 如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7)
如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7) 如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC. 请你根据如图所示已知条件,推想正确结论,要求每个结论同时含有字母a,b.写出至少三条正确结论:b>a,ab>0,a+b<0.
请你根据如图所示已知条件,推想正确结论,要求每个结论同时含有字母a,b.写出至少三条正确结论:b>a,ab>0,a+b<0.