题目内容
11.解下列方程组:(1)$\left\{\begin{array}{l}{x+y=3}\\{y+z=5}\\{x+z=6}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x+2y+z=14}\\{x+y+z=10}\\{2x+3y-z=1}\end{array}\right.$.
分析 (1)显然用加减消元法求解可得;
(2)①-②、①+③消去z得到关于x、y的二元一次方程组,解方程组可得x、y的值,将求得的x、y的值代回方程②可得z的值.
解答 解:(1)解方程组$\left\{\begin{array}{l}{x+y=3}&{①}\\{y+z=5}&{②}\\{x+z=6}&{③}\end{array}\right.$,
①-②,得:x-z=-2 ④,
③+④,得:2x=4,解得:x=2,
将x=2代入①,得:y=1,
将x=2代入③,得:z=4,
所以方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=4}\end{array}\right.$;
(2)解方程组$\left\{\begin{array}{l}{3x+2y+z=14}&{①}\\{x+y+z=10}&{②}\\{2x+3y-z=1}&{③}\end{array}\right.$,
①-②,得:2x+y=4 ④,
①+③,得:5x+5y=15,即x+y=3 ⑤,
④-⑤,得:x=1,
将x=1代入⑤,得:y=2,
将x=1,y=2代入②,得:z=7,
所以方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=7}\end{array}\right.$.
点评 本题主要考查了三元一次方程组的解法,①首先利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组.②然后解这个二元一次方程组,求出这两个未知数的值.③再把求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个关于第三个未知数的一元一次方程.④解这个一元一次方程,求出第三个未知数的值.⑤最后将求得的三个未知数的值用“{,”合写在一起即可.

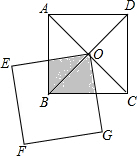 如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )| A. | 由小变大 | B. | 由大变小 | ||
| C. | 始终不变 | D. | 先由大变小,然后又由小变大 |
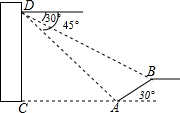 如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号).
如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号).