题目内容
12.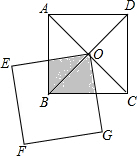 如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )| A. | 由小变大 | B. | 由大变小 | ||
| C. | 始终不变 | D. | 先由大变小,然后又由小变大 |
分析 根据正方形的性质得出OB=OC,∠OBC=∠OCD=45°,∠BOC=∠EOG=90°,推出∠BON=∠MOC,证出△OBN≌△OCM.
解答 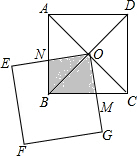 解:重叠部分面积不变,总是等于正方形面积的$\frac{1}{4}$.
解:重叠部分面积不变,总是等于正方形面积的$\frac{1}{4}$.
理由如下:
∵四边形ABCD和四边形OEFG都是正方形,
∴OB=OC,∠OBC=∠OCD=45°,∠BOC=∠EOG=90°,
∴∠BON=∠MOC.
在△OBN与△OCM中,
$\left\{\begin{array}{l}{∠OBC=∠OCD}\\{OB=OC}\\{∠BON=∠MOC}\end{array}\right.$,
∴△OBN≌△OCM(ASA),
∴四边形OMCN的面积等于三角形BOC的面积,
即重叠部分面积不变,总是等于正方形面积的$\frac{1}{4}$.
故选C.
点评 本题考查对正方形的性质,全等三角形的性质和判定等知识点的理解和掌握,能推出四边形OMCN的面积等于三角形BOC的面积是解此题的关键.

练习册系列答案
相关题目
13.要时分式$\frac{{x}^{2}-4}{x+2}$有意义,则x应满足的条件为( )
| A. | x≠2 | B. | x≠0 | C. | x≠±2 | D. | x≠-2 |
14.已知二次函数y=ax2+bx+c的图象过(-1,2)且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1,下列结论正确的有( )
(1)4a-2b+c<0 (2)2a-b<0 (3)a>-1 (4)b2+8a>4ac.
(1)4a-2b+c<0 (2)2a-b<0 (3)a>-1 (4)b2+8a>4ac.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
| A. | 小明的影子比小强的影子长 | B. | 小明的影子比小强的影子短 | ||
| C. | 小明的影子和小强的影子一样长 | D. | 两人的影子长度不确定 |
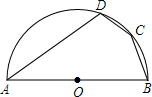 已知,如图所示,C,D是以AB为直径的半圆O上的两点,且DC=BC=$\frac{1}{4}$AB=1.求AD的长.
已知,如图所示,C,D是以AB为直径的半圆O上的两点,且DC=BC=$\frac{1}{4}$AB=1.求AD的长.