题目内容
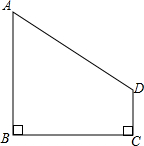 如图,在四边形ABCD中,AB⊥BC,DC⊥BC.当AB=4,DC=1,BC=4时,在BC上是否存在点P,使得AP⊥PD?若存在,求线段BP的长;若不存在,请说明理由.
如图,在四边形ABCD中,AB⊥BC,DC⊥BC.当AB=4,DC=1,BC=4时,在BC上是否存在点P,使得AP⊥PD?若存在,求线段BP的长;若不存在,请说明理由.考点:相似三角形的判定与性质
专题:
分析:利用△ABP∽△PCD得出∠BPA+∠DPC=90°,即∠APD=90°,求出BP的长即可.
解答: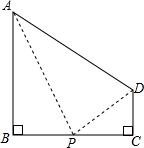 解:存在.
解:存在.
如图所示,AP⊥PD,
∴∠APD=90°,
∴∠APB+∠DPC=90°,
又∵DC⊥BC,
∴∠DCP=90°,
∴∠PDC+∠DPC=90°,
∴∠APB=∠PDC,
∵∠B=∠C,
∴△ABP∽△PCD,
设BP=x,则CP=4-x,
∴
=
,即4:(4-x)=x:1,
即x(4-x)=4,
则x2-4x+4=0,
即(x-2)2=0,
得出x=2,即BP=2.
 解:存在.
解:存在.如图所示,AP⊥PD,
∴∠APD=90°,
∴∠APB+∠DPC=90°,
又∵DC⊥BC,
∴∠DCP=90°,
∴∠PDC+∠DPC=90°,
∴∠APB=∠PDC,
∵∠B=∠C,
∴△ABP∽△PCD,
设BP=x,则CP=4-x,
∴
| AB |
| PC |
| BP |
| DC |
即x(4-x)=4,
则x2-4x+4=0,
即(x-2)2=0,
得出x=2,即BP=2.
点评:此题主要考查了相似三角形的判定与性质,得出△ABP∽△PCD进而求出是解题关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
福布斯中文网微博通报数据显示,天猫双11成交额已经在活动开始后的60分钟内突破122亿元人民币.则122亿用科学记数法来表示是( )
| A、1.22×1010 |
| B、122×108 |
| C、12.2×109 |
| D、1.22×109 |
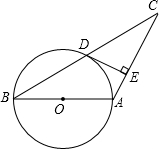 如图,等腰△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,DE⊥AC于点E.
如图,等腰△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,DE⊥AC于点E. 有甲乙两根木杆,线段BC是甲木杆的投影,在图中画出形成投影的太阳光线及乙木杆的投影.
有甲乙两根木杆,线段BC是甲木杆的投影,在图中画出形成投影的太阳光线及乙木杆的投影.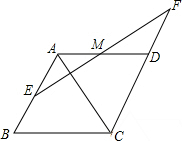 如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF交AD于M,交CD的延长线于点F.
如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF交AD于M,交CD的延长线于点F. 已知AD=AE,AF=AG,AD⊥BD,AE⊥CE,求证:AB=AC.
已知AD=AE,AF=AG,AD⊥BD,AE⊥CE,求证:AB=AC.