题目内容
 如图,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠E与∠A的关系.
如图,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠E与∠A的关系.考点:三角形内角和定理,三角形的外角性质
专题:
分析:证明∠ACE=∠BCE(设为α),∠ABE=∠DBE;进而证明∠DBE=α+∠E,∠DBE=
=
∠A+α,得到α+∠E=α+
∠A,即可解决问题.
| ∠A+2α |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:∵CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,
解:∵CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,
∴∠ACE=∠BCE(设为α),∠ABE=∠DBE,
∵∠DBE=α+∠E,∠DBE=
=
∠A+α,
∴α+∠E=α+
∠A,
∴∠A=2∠E.
 解:∵CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,
解:∵CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,∴∠ACE=∠BCE(设为α),∠ABE=∠DBE,
∵∠DBE=α+∠E,∠DBE=
| ∠A+2α |
| 2 |
| 1 |
| 2 |
∴α+∠E=α+
| 1 |
| 2 |
∴∠A=2∠E.
点评:该题以三角形为载体,主要考查了三角形的内角和定理、外角的性质及其应用问题;灵活运用三角形的内角和定理、外角的性质是解题的关键.

练习册系列答案
相关题目
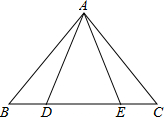 如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案:
如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: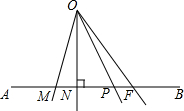 如图,过直线AB外一点O,画射线OM,ON,OP,OF,分别交AB于点M,N,P,F,其中ON⊥AB于点N,则能表示点O到直线AB的距离的是线段
如图,过直线AB外一点O,画射线OM,ON,OP,OF,分别交AB于点M,N,P,F,其中ON⊥AB于点N,则能表示点O到直线AB的距离的是线段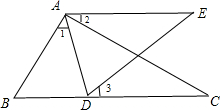 如图,在△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.若AE∥BC,且∠E=∠CAD,求∠C的度数.
如图,在△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.若AE∥BC,且∠E=∠CAD,求∠C的度数.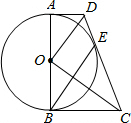 如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,以AB为直径作⊙O,恰与CD相切于点E,连接OD,OC,BE,
如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,以AB为直径作⊙O,恰与CD相切于点E,连接OD,OC,BE,